Giải mục I trang 88, 89 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Đề bài
Luyện tập – vận dụng 1 trang 89 Sách giáo khoa Toán 10 – Cánh Diều
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Tìm các số a, b biết: \(\overrightarrow {AG} = a.\overrightarrow {AM} ;\overrightarrow {GN} = b.\overrightarrow {GB} \)
Phương pháp giải - Xem chi tiết
Từ đẳng thức vecto suy ra hướng và độ dài của hai vecto.
Lời giải chi tiết
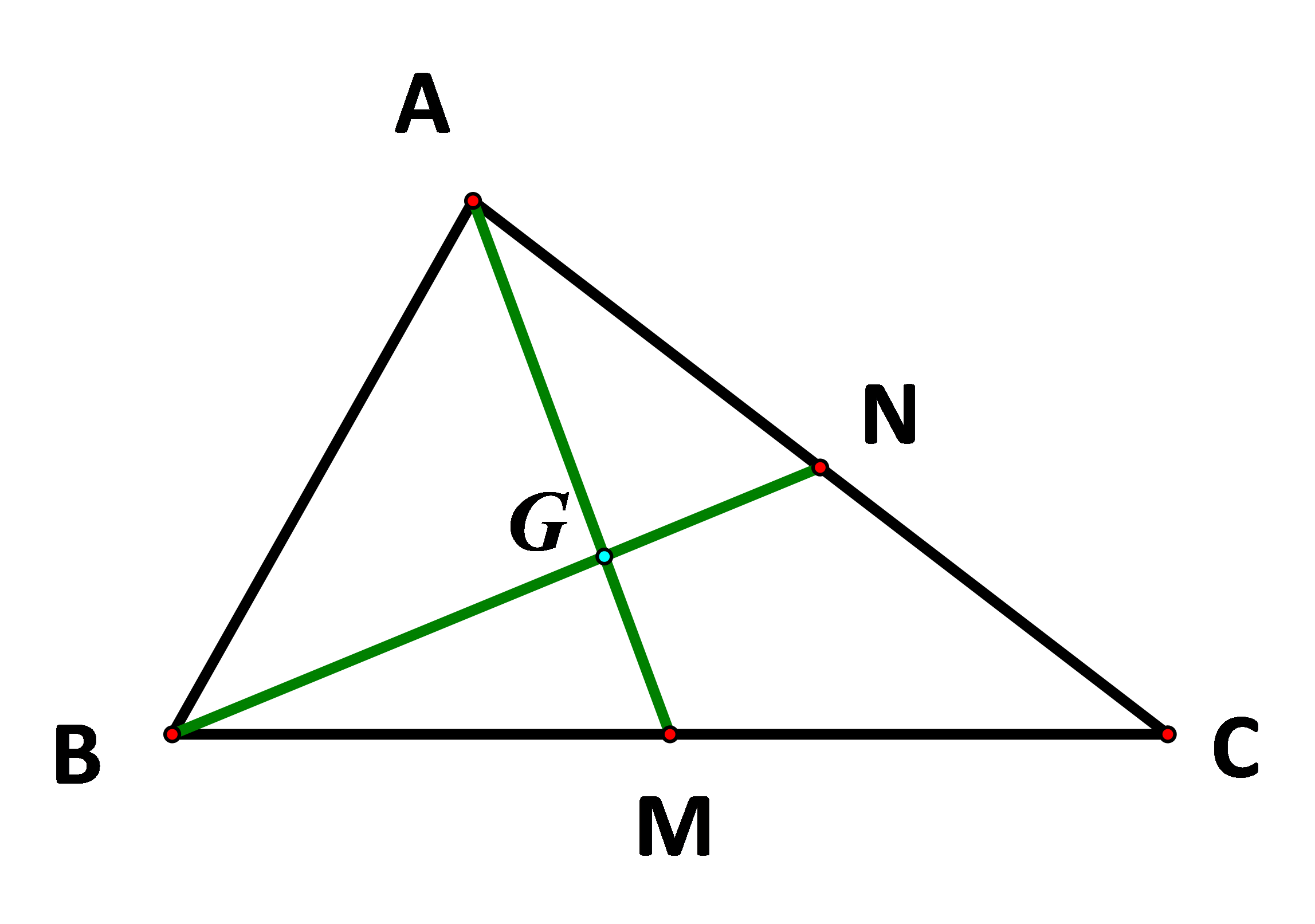
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)
Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]
Suy ra \(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b = - \frac{1}{2}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục I trang 88, 89 SGK Toán 10 tập 1 - Cánh diều timdapan.com"







