Giải mục I trang 12, 13 SGK Toán 10 tập 1 - Cánh diều
Hãy nêu cách cho một tập hợp. Người ta còn minh họa tập hợp bằng một vòng kín, Nêu số phần tử của mỗi tập hợp sau
Hoạt động 1
Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp.
Lời giải chi tiết:
Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}
Hoạt động 2
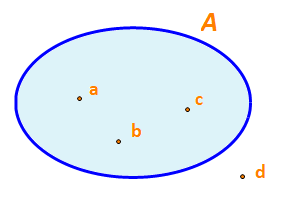
Người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Phương pháp giải:
a) Liệt kê các phần tử biểu thị bởi chấm bên trong vòng kín.
b) Xác định các phần tử không thuộc A (các chấm bên ngoài vòng kín)
Lời giải chi tiết:
a) Tập hợp A là: A = {a; b; c}
b) Phần tử không thuộc tập hợp A là: d.
Hoạt động 3
Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Luyện tập – vận dụng 1
Nêu số phần tử của mỗi tập hợp sau:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} ,\) \(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} \). Tập hợp G không chứa phần tử nào vì \({x^2} - 2 = 0 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb{Z}\)
\(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\): tập hợp N* có vô số phần tử.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục I trang 12, 13 SGK Toán 10 tập 1 - Cánh diều timdapan.com"







