Giải mục I trang 112, 113 SGK Toán 7 tập 2 - Cánh diều

I. Đường trung trực của tam giác

HĐ 1

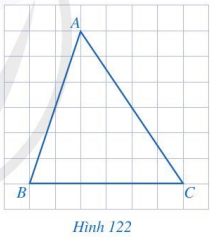
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.

Phương pháp giải:

Đường trung trực là đường thẳng đi qua trung điểm của cạnh và vuông góc cạnh tại trung điểm đó.

Lời giải chi tiết:

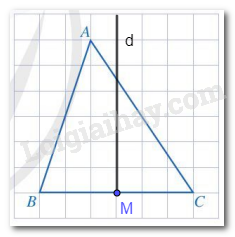
Lấy M là trung điểm của đoạn thẳng BC. Đường thẳng d là đường thẳng đi qua M và vuông góc với BC.

LT - VD 1

Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.

Phương pháp giải:

Chứng minh AD là đường trung trực của tam giác ABC ta chứng minh D là trung điểm của BC và \(AD \bot BC\)

Lời giải chi tiết:

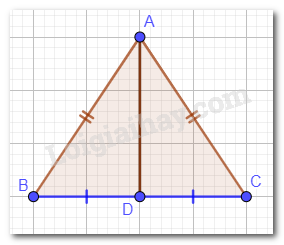
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).

Xét tam giác ABD và tam giác ACD có:

     AB = AC (tam giác ABC cân tại A);

     \(\widehat {BAD} = \widehat {CAD}\);

     AD chung

Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)

\(\Rightarrow\) D là trung điểm của cạnh BC.

Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).

Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ  \Rightarrow AD \bot BC\).

Vậy AD là đường trung trực của tam giác ABC.