Giải mục 3 trang 65, 66 SGK Toán 7 tập 2 - Chân trời sáng tạo
Quan sát tam giác AHB ở Hình 6. a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn b) Từ câu a, hãy giải thích vì sao AB > AH.
HĐ 3
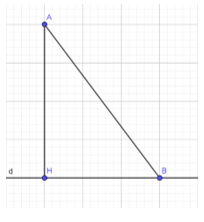
Quan sát tam giác AHB ở Hình 6.
a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao AB > AH.
Phương pháp giải:
- Ta sử dụng định lí về tổng số đo 3 góc
- Ta sử dụng tính chất góc đói diện cạnh lớn hơn thì lớn hơn
Lời giải chi tiết:
a) Xét tam giác AHB vuông tại H ( theo giả thiết )
\( \Rightarrow \widehat {AHB} = {90^o}\)
\( \Rightarrow \widehat {ABH} + \widehat {HAB} = {90^o}\)( Do tổng số đo 3 góc = 180°;\(\widehat H + \widehat B + \widehat A = {180^o}\))
\( \Rightarrow \widehat {AHB} > \widehat {ABH}\)( Do \(\widehat {AHB} = {90^o}\)và \(\widehat {ABH} < {90^o}\))
b)Theo định lí góc đối diện với cạnh lớn hơn thì lớn hơn trong tam giác ta có :
\(\widehat {AHB} > \widehat {ABH}\)( chứng minh a )
Và \(\widehat {AHB}\) đối diện với AB, \(\widehat {ABH}\) đối diện với AH
\( \Rightarrow AB > AH\)
Thực hành 2
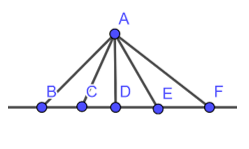
Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên
Lời giải chi tiết:
Theo hình 8 ta thấy AD là đường ngắn nhất vì AD vuông góc với BF
Các đường xiên là AB, AC, AE, AF.
Vận dụng 2
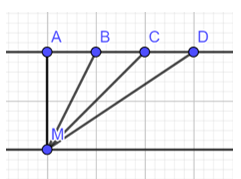
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.
Lời giải chi tiết:
Ta gọi thành hồ bơi đối diện là đường thẳng AD
Bạn Minh bơi đường ngắn nhất khi bơi từ điểm M 1 đường vuông góc với AD do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
Ta thấy AM vuông góc AD nên AM là đường ngắn nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 65, 66 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







