Giải mục 1 trang 64 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC trong Hình 1. - Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c - Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c. - Nêu nhận xét của em về hai kết quả sắp xếp trên.
HĐ 1
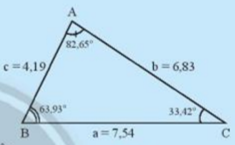
Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
Phương pháp giải:
Ta dựa cào số đo các cạnh, góc của tam giác để sắp xếp theo độ lớn
Lời giải chi tiết:
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
Thực hành 1
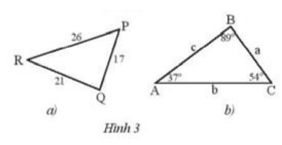
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.
Phương pháp giải:
Sử dụng định lí về góc đối diện cạnh trong tam giác
Lời giải chi tiết:
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.
Vận dụng 1
a) Cho tam giác DEF có góc F là góc tù. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF ?
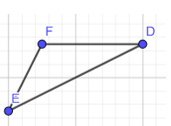
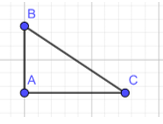
b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC ?
Phương pháp giải:
Sử dụng tính chất góc đối diện và cạnh trong tam giác
Lời giải chi tiết:
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 64 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







