Giải mục 3 trang 60,61,62 SGK Toán 12 tập 1 - Chân trời sáng tạo

Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo

KP3

Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo

Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.

Phương pháp giải:

Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a  - \overrightarrow b  = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)

Lời giải chi tiết:

\(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA}  = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)

TH3

Trả lời câu hỏi Thực hành 3 trang 61 SGK Toán 12 Chân trời sáng tạo

Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).

a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)

b) Tính các độ dài MN, NP, MP.

Phương pháp giải:

a) Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a  - \overrightarrow b  = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)

b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)

Lời giải chi tiết:

a) \(\overrightarrow {MN}  = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)

\(\overrightarrow {NP}  = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)

\(\overrightarrow {MP}  = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)

b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}}  = 2\sqrt {69} \)

\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}}  = \sqrt {118} \)

\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}}  = 3\sqrt {10} \)

KP4

Trả lời câu hỏi Khám phá 4 trang 61 SGK Toán 12 Chân trời sáng tạo

Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM}  = \frac{1}{2}(\overrightarrow {OA}  + \overrightarrow {OB} )\),\(\overrightarrow {OG}  = \frac{1}{3}(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.

Phương pháp giải:

Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a  + \overrightarrow b  = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)

Lời giải chi tiết:

\(\overrightarrow {OA}  + \overrightarrow {OB}  = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)

\(\overrightarrow {OM}  = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)

\(\overrightarrow {OG}  = \frac{1}{3}(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)

TH4

Trả lời câu hỏi Thực hành 4 trang 62 SGK Toán 12 Chân trời sáng tạo

Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:

a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;

b) Trọng tâm G của tam giác M′N′P′.

Phương pháp giải:

Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

Lời giải chi tiết:

a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)

\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).

\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)

b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)

VD3

Trả lời câu hỏi Vận dụng 3 trang 62 SGK Toán 12 Chân trời sáng tạo

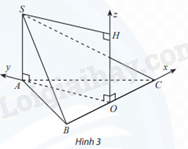
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:

a) Các điểm A, S, B, C

b) Trung điểm M của SB và trung điểm N của SC;

c) Trọng tâm G của tam giác SBC

Phương pháp giải:

\(\overrightarrow {OA}  = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

Lời giải chi tiết:

a) \(OA = \sqrt {A{B^2} - O{B^2}}  = \sqrt {{a^2} - {{(\frac{a}{2})}^2}}  = \frac{{a\sqrt 3 }}{2}\)

\(\overrightarrow {OA}  = \frac{{a\sqrt 3 }}{2}\overrightarrow j  = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)

\(\overrightarrow {OB}  =  - \frac{a}{2}\overrightarrow i  = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)

\(\overrightarrow {OC}  = \frac{a}{2}\overrightarrow i  = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)

\(\overrightarrow {OS}  = \frac{{a\sqrt 3 }}{2}\overrightarrow j  + a\overrightarrow k  = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)

b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)

\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)

c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)

TH5

Trả lời câu hỏi Thực hành 5 trang 63 SGK Toán 12 Chân trời sáng tạo

Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).

a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.

b) Tìm độ dài cạnh MN và MP.

c) Tính góc M

Phương pháp giải:

a) \(\overrightarrow a  \bot \overrightarrow b  \Rightarrow \overrightarrow a .\overrightarrow b  = 0\)

b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)

c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải chi tiết:

a) Ta có: \(\overrightarrow {NP}  = (2; - 1; - 1)\)

Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP

=> \(\overrightarrow {NK}  = (x - 5;y - 9;z - 3)\)

\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 =  - t;z - 3 =  - t\) => \(K(2t + 2; - t + 9; - t + 3)\)

Ta có: \(\overrightarrow {MK}  = (2t + 2; - t + 8; - t + 1)\)

\(\overrightarrow {MK}  \bot \overrightarrow {NP}  \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP}  = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)

Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)

b) Ta có: \(\overrightarrow {MN}  = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}}  = 3\sqrt {10} \)

\(\overrightarrow {MP}  = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}}  = 7\sqrt 2 \)

c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)

VD4

Trả lời câu hỏi Vận dụng 4 trang 64 SGK Toán 12 Chân trời sáng tạo

Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:

a) Các khoảng cách giữa mỗi cặp drone giao hàng.

b) Góc \(\widehat {BAC}\)

Phương pháp giải:

a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)

b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải chi tiết:

a) \(\overrightarrow {AB}  = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}}  = 2\sqrt {29} \)

\(\overrightarrow {AC}  = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}}  = \sqrt {173} \)

\(\overrightarrow {BC}  = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}}  = \sqrt {57} \)

c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)