Giải mục 3 trang 100, 101 SGK Toán 10 tập 1 - Chân trời sáng tạo
Cho hai vectơ i, j vuông góc có cùng độ dài bằng 1. Phân tử sulfur dioxide SO2 có cấu tạo hình chữ V, góc liên kết OSO gần bằng 120
Thực hành 4
Cho hai vectơ \(\overrightarrow i ,\overrightarrow j \) vuông góc có cùng độ dài bằng 1.
a) Tính \({\left( {\overrightarrow i + \overrightarrow j } \right)^2};{\left( {\overrightarrow i - \overrightarrow j } \right)^2};\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right)\).
b) Cho \(\overrightarrow a = 2\overrightarrow i + 2\overrightarrow j ,\overrightarrow b = 3\overrightarrow i - 3\overrightarrow j \). Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) và tính góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Phương pháp giải:
Sử dụng các tính chất của tích vô hướng giữa các vectơ
Lời giải chi tiết:
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
Vận dụng 2
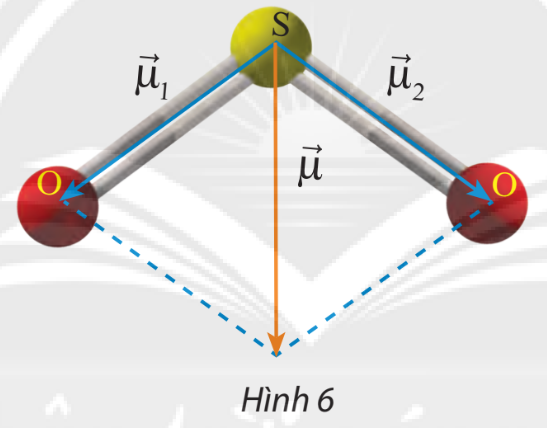
Phân tử sulfur dioxide \((S{O_2})\) có cấu tạo hình chữ V, góc liên kết \(\widehat {OSO}\) gần bằng \(120^\circ \). Người ta biểu diễn sự phân cực giữa nguyên tử S và nguyên tử O bằng các vectơ \(\overrightarrow {{\mu _1}} \)và \(\overrightarrow {{\mu _2}} \) có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng\(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} \) được dùng để biểu diễn sự phân cực của cả phân tử \(\)SO2. Tính độ dài của \(\overrightarrow \mu \).
Phương pháp giải:
Sử dụng kết quả của ví dụ 4 trang 101 \({c^2} = {a^2} + {b^2} - 2bc.\cos C\)
Lời giải chi tiết:
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 100, 101 SGK Toán 10 tập 1 - Chân trời sáng tạo timdapan.com"