Giải mục 2 trang 49 SGK Toán 9 tập 2 - Cánh diều
a) Nêu khái niệm đồ thị của hàm số \(y = f(x)\). b) Xét hàm số \(y = 2{x^2}\). Hãy thực hiện các hoạt động sau: - Tìm giá trị của y tương ứng với giá trị của x trong bảng sau: - Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên. - Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số\(y = 2{x^2}\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 49 SGK Toán 9 Cánh diều
a) Nêu khái niệm đồ thị của hàm số \(y = f(x)\).
b) Xét hàm số \(y = 2{x^2}\). Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.
- Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y = 2{x^2}\).
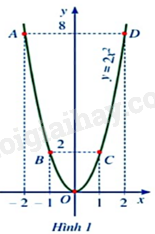
c) Xét hàm số \(y = - 2{x^2}\). Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
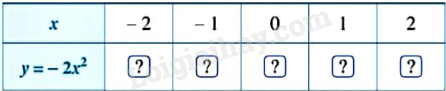
- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.
- Quan sát Hình 2, vẽ vẽ đường cong như ở Hình 2 đi qua 5 điểm M, N, O, P, Q. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y = - 2{x^2}\).
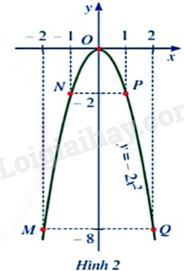
Phương pháp giải:
a) Nhớ lại định nghĩa đồ thị hàm số lớp 8.
b), c) Bước 1: Thay từng giá trị x vào hàm số \(y = 2{x^2}\) ta tìm được giá trị y tương ứng.
Bước 2: Vẽ hệ trục tọa độ Oxy và biểu diễn tọa độ từng điểm trên mặt phẳng tọa độ.
Bước 3: Nối các điểm trên ta được đồ thị của hàm số.
Lời giải chi tiết:
a) Đồ thị của hàm số \(y = f(x)\) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng \((x;f(x))\) trên mặt phẳng tọa độ.
b)
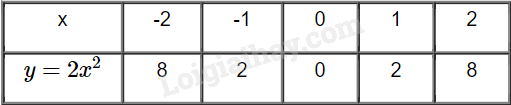
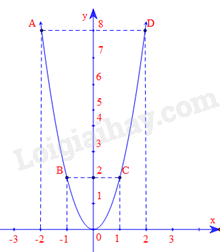
Các điểm A(-2;8), B(-1;2), O(0;0), C(1;2), D(2;8)
Đồ thị của hàm số \(y = 2{x^2}\):
c)
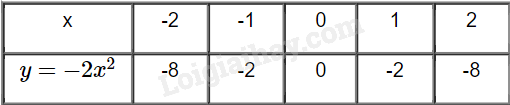
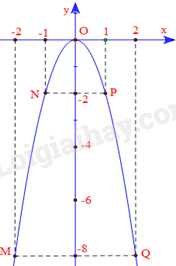
Các điểm A(-2;-8), B(-1;-2), O(0;0), C(1;-2), D(2;-8)
Đồ thị của hàm số \(y = - 2{x^2}\):
LT3
Trả lời câu hỏi Luyện tập 3 trang 49 SGK Toán 9 Cánh diều
Vẽ đồ thị của hàm số \(y = - 3{x^2}\)
Phương pháp giải:
- Lập bảng giá trị của y tương ứng với giá trị của x giá trị của x (lấy ít nhất 5 điểm).
- Vẽ đồ thị hàm số đi qua 5 điểm đó, ta được parabol cần tìm.
Lời giải chi tiết:
Ta có bảng giá trị:
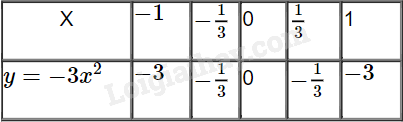
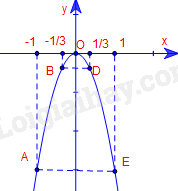
Vẽ các điểm \(A( - 1; - 3),B( - \frac{1}{3}; - \frac{1}{3}),O(0;0),D(\frac{1}{3}; - \frac{1}{3}),E(1; - 3)\) thuộc đồ thị của hàm số \(y = - 3{x^2}\)trong mặt phẳng tọa độ Oxy.
Vẽ đường parabol đi qua 5 điểm A,B,O,D,E ta nhận được đồ thị của hàm số \(y = - 3{x^2}\).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 49 SGK Toán 9 Cánh diều
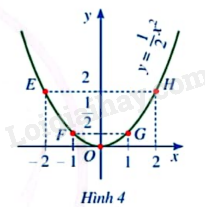
Quan sát đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H, F và G đối với trục Oy.
Phương pháp giải:
Chú ý về tính đối xứng của các cặp điểm so với trục Oy.
Lời giải chi tiết:
Điểm E đối xứng với H, F đối xứng với G qua Oy.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 49 SGK Toán 9 tập 2 - Cánh diều timdapan.com"







