Giải mục 1 trang 94, 95 SGK Toán 10 tập 1 - Chân trời sáng tạo
Hãy xác định độ dài và hướng của hai vectơ Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ.
HĐ Khám phá 1
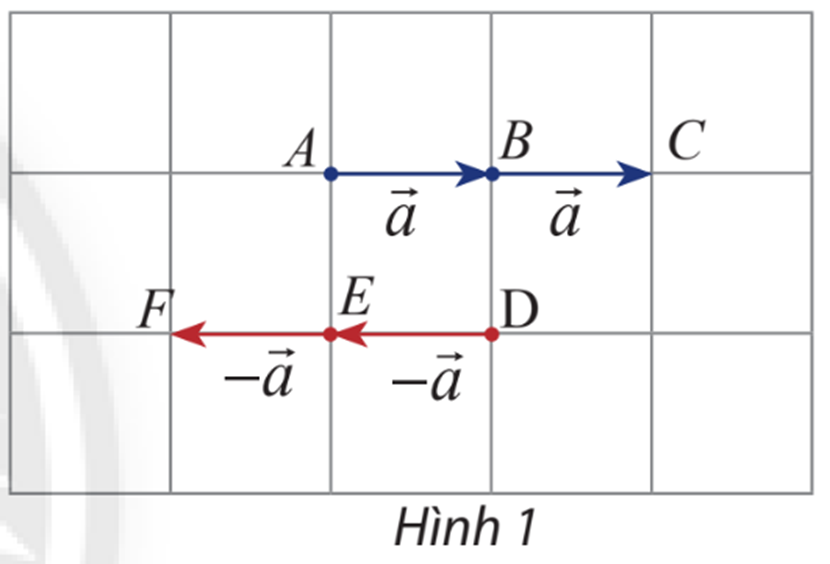
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
Lời giải chi tiết:
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
Thực hành 1
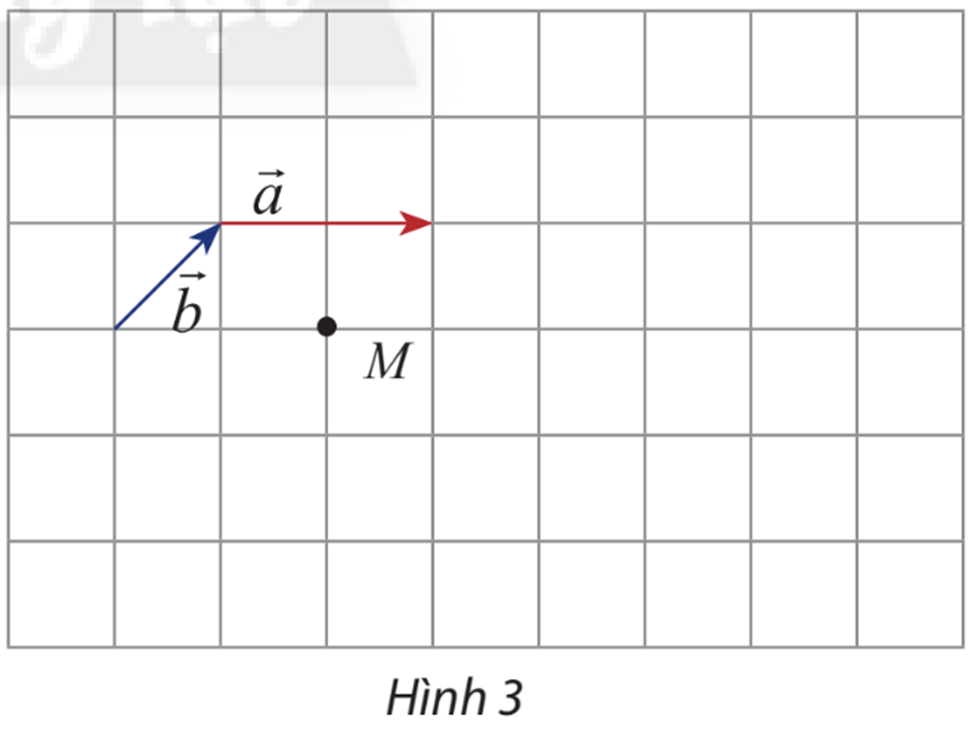
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
Phương pháp giải:
Bước 1: Xác định hướng của vectơ \(\overrightarrow a ;\overrightarrow b \)
Bước 2: Xác định tỉ lệ độ dài \(\frac{{\left| {\overrightarrow x } \right|}}{{\left| {\overrightarrow a } \right|}}\)
Lời giải chi tiết:
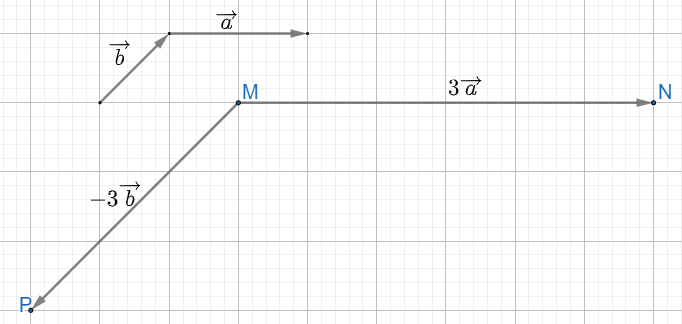
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
Thực hành 2
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Phương pháp giải:
Sử dụng quy tắc 3 điểm \(\overrightarrow {MA} = \overrightarrow {MG} + \overrightarrow {GA}\)
Lời giải chi tiết:
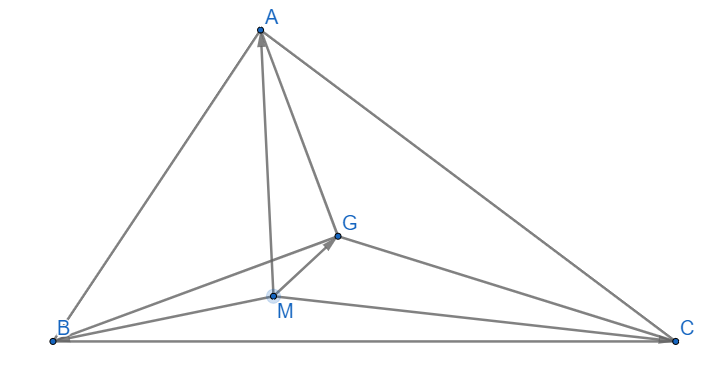
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \Leftrightarrow \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG} \)
\( \Leftrightarrow \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \)
\( \Leftrightarrow 3\overrightarrow {MG} = 3\overrightarrow {MG} \) (đpcm) ( Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
Vận dụng
Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của tàu B theo vectơ vận tốc \(\overrightarrow a \) của tòa A.

Lời giải chi tiết:
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)

Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 94, 95 SGK Toán 10 tập 1 - Chân trời sáng tạo timdapan.com"







