Giải mục 1 trang 54, 55 Chuyên đề học tập Toán 10 - Kết nối tri thức
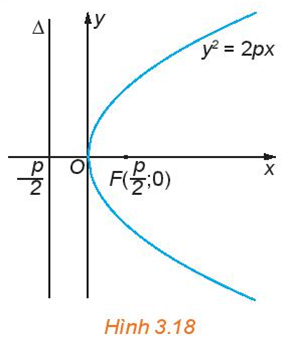
Cho parabol có phương trình chính tắc \(y = 2px\) (H.3.18).
HĐ1
Cho parabol có phương trình chính tắc \(y = 2px\) (H.3.18).
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì điểm \(N({x_0}; - {y_0})\) có thuộc parabol hay không?
b) Từ phương trình chính tắc của parabol, có thể rút ra điều gì về hoành độ của những điểm thuộc parabol?
Lời giải chi tiết:
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)
nên điểm \(N({x_0}; - {y_0})\) có thuộc parabol.
b)
Với p>0 thì các điểm thuộc paranol đều có hoành độ \( \ge 0\).
Luyện tập 1
Trongg mặt phẳng tọa độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm A(6;6). Tìm tham số tiêu và phương trình đường chuẩn của (P)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tham số tiêu: p
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
Gọi PTCT của (P) là \({y^2} = 2px\)
Vì \(A\left( {6;6} \right) \in (P)\) nên \({6^2} = 2.p.6 \Rightarrow p = 3\)
+ Tham số tiêu: p = 3
+ Đường chuẩn: \(\Delta :x = - \frac{3}{2}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 54, 55 Chuyên đề học tập Toán 10 - Kết nối tri thức timdapan.com"







