Giải mục 1 trang 38, 39, 40 SGK Toán 11 tập 2 - Kết nối tri thức

Hoạt động 1

Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.

a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song hay không?

b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?

Phương pháp giải:

Quan sát thực tế

Lời giải chi tiết:

a) Bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song với tia nắng mặt trời.

b) Khi tia sáng mặt trời vuông góc với mặt sân, bóng của cây cột sẽ không xuất hiện trên mặt sân vì không có tia sáng nào có thể chiếu trực tiếp lên bề mặt sân để tạo ra bóng của cây cột.

Hỏi chấm 1

a) Nếu A là một điểm không thuộc mặt phẳng (P) và A’ là hình chiếu của A trên (P) thì đường thẳng AA’ có quan hệ gì với mặt phẳng (P)?

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì?

Phương pháp giải:

Phép chiếu song song lên mặt phẳng (P) theo phương \(\Delta \) vuông góc với (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).

Lời giải chi tiết:

a) AA’ vuông góc với mặt phẳng (P)

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là giao điểm của a với (P).

Hoạt động 2

Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tuỳ ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34).

a) Hình chiếu của a trên mặt phẳng (P) là đường thẳng nào?

b) Nếu b vuông góc với M'N' thì b có vuông góc với a hay không?

c) Nếu b vuông góc với a thì b có vuông góc với M'N' hay không?

Phương pháp giải:

Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với 2 đường thẳng cắt nhau nằm trong mặt phẳng đó.

Lời giải chi tiết:

a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.

b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.

c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.

Luyện tập 1

Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).

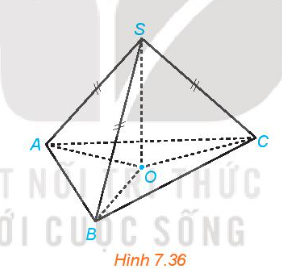
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.

b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).

c) Chứng minh rằng nếu \(AO \bot BC\) thì \(SA \bot BC.\)

d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)

Phương pháp giải:

- Sử dụng định lý Pytago

- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Lời giải chi tiết:

a) O là hình chiếu của S trên mặt phẳng (ABC) nên \(SO \bot \left( {ABC} \right)\)

Mà \(OA,OB,OC \subset \left( {ABC} \right) \Rightarrow SO \bot OA,SO \bot OB,SO \bot OC\)

Xét tam giác SAO vuông tại O \(\left( {SO \bot OA} \right)\) có

\(S{A^2} = O{A^2} + S{O^2}\) (Định lí Pytago)

Xét tam giác SBO vuông tại O \(\left( {SO \bot OB} \right)\) có

\(S{B^2} = O{B^2} + S{O^2}\) (Định lí Pytago)

Xét tam giác SCO vuông tại O \(\left( {SO \bot OC} \right)\) có

\(S{C^2} = O{C^2} + S{O^2}\) (Định lí Pytago)

Mà SA = SB = SC nên OA = OB = OC

Do đó O là tâm đường trọn ngoại tiếp tam giác ABC.

b) O là hình chiếu của S trên mặt phẳng (ABC)

A là hình chiếu của A trên mặt phẳng (ABC)

\( \Rightarrow \) OA là hình chiếu của SA trên mặt phẳng (ABC)

c) \(\left. \begin{array}{l}AO \bot BC\\SO \bot BC\left( {SO \bot \left( {ABC} \right)} \right)\\AO \cap SO = \left\{ O \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAO} \right);SA \subset \left( {SAO} \right) \Rightarrow SA \bot BC\)

d) O là hình chiếu của S trên mặt phẳng (ABC)

A là hình chiếu của A trên mặt phẳng (ABC)

B là hình chiếu của B trên mặt phẳng (ABC)

C là hình chiếu của C trên mặt phẳng (ABC)

\( \Rightarrow \) Tam giác OAB là hình chiếu của tam giác SAB trên mặt phẳng (ABC)

Tam giác OBC là hình chiếu của tam giác SBC trên mặt phẳng (ABC)

Tam giác OCA là hình chiếu của tam giác SCA trên mặt phẳng (ABC)