Giải mục 1 trang 31, 32 SGK Toán 8 tập 2 – Chân trời sáng tạo

HĐ1

a) Ở câu hỏi khởi động trên, viết các biểu thức biểu thị tổng khối lượng của các vật trên mỗi đĩa cân. Từ điểu kiện cân thăng bằng, hai biểu thức có mối quan hệ như thế nào?

b) Nếu \(x = 200\)thì cân có cân bằng không? Tại sao?

Nếu \(x = 100\) thì cân có cân bằng không? Tại sao?

Phương pháp giải:

Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.

Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.

Lời giải chi tiết:

a) Trên đĩa cân bên trái ta thấy có 4 quả cân, mỗi quả có khối lượng \(x\) gam nên khối lượng đĩa cân bên trái là: \(x + x + x + x\) (gam)

Trên đĩa cân bên phải ta thấy có 2 quả cân, một quả có khối lượng \(x\) gam và một quả có khối lượng 600 gam nên khối lượng đĩa cân bên phải là: \(x + 600\) gam.

Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:

\(x + x + x + x = x + 600\) hay \(4x = 600 + x\)

b) Nếu \(x = 200\) thì khối lượng đĩa cân bên trái là: \(4.200 = 800\) (gam); khối lượng đĩa cân bên phải là \(200 + 600 = 800\) (gam).

Do đó, cân thăng bằng.

Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(4.100 = 400\) (gam); khối lượng đĩa cân bên phải là \(100 + 600 = 700\) (gam).

Do đó, cân không thăng bằng.

Thực hành 1

Cho phương trình \(4t - 3 = 12 - t\). Trong hai số 3 và 5, có số nào là nghiệm của phương trình đã cho không?

Phương pháp giải:

Giá trị \({x_0}\)của biến \(x\) làm cho hai vế của phương trình bằng nhau được gọi là nghiệm của phương trình.

Lời giải chi tiết:

+ Với \(t = 3\) thay vào phương trình ta được

\(4.3 - 3 = 12 - 3\) hay \(9 = 9\) (đúng)

Do đó, \(t = 3\) là nghiệm của phương trình.

+ Với \(t = 5\) thay vào phương trình ta được

\(4.5 - 3 = 12 - 5\) hay \(17 = 7\) (sai)

Do đó, \(t = 5\) không là nghiệm của phương trình.

Vận dụng 1

Đặt lên hai đĩa cân những quả cân như Hình 1.

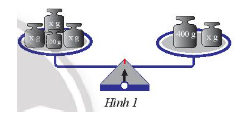
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.

b) Nếu \(x = 100\) cân có thăng bằng không? Vì sao?

Nếu \(x = 150\) thì cân có thăng bằng không? Vì sao?

Từ đó, chỉ ra một nghiệm của phương trình ở câu a.

Phương pháp giải:

Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.

Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.

Lời giải chi tiết:

a) Trên đĩa cân bên trái ta thấy có 4 quả cân, có 3 quả có khối lượng \(x\) gam và 1 quả có khối lượng 100 gam nên khối lượng đĩa cân bên trái là: \(x + x + x + 100\) (gam)

Trên đĩa cân bên phải ta thấy có 2 quả cân, 1 quả có khối lượng \(x\) gam và một quả có khối lượng 400 gam nên khối lượng đĩa cân bên phải là: \(x + 400\) gam.

Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:

\(x + x + x + 100 = x + 400\) hay \(3x + 100 = 400 + x\).

Vậy phương trình biểu diễn sự thăng bằng là \(3x + 100 = 400 + x\).

b) Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(3.100 + 100 = 300 + 100 = 400\) (gam); khối lượng đĩa cân bên phải là \(400 + 100 = 500\) (gam).

Do đó, cân không thăng bằng.

Nếu \(x = 150\) thì khối lượng đĩa cân bên trái là: \(3.150 + 100 = 550\) (gam); khối lượng đĩa cân bên phải là \(150 + 400 = 550\) (gam).

Do đó, cân thăng bằng.