Giải mục 1 trang 136, 137 SGK Toán 11 tập 1 - Chân trời sáng tạo

Hoạt động 1

a) Sử dụng biểu đồ ở Hoạt động mở đầu, hoàn thiện bảng thống kê sau:

b) Tìm các nhóm chứa giá trị trung vị chiều cao thành viên mỗi đội.

Phương pháp giải:

Quan sát biểu đồ và điền vào bảng.

Lời giải chi tiết:

a)

b) Nhóm chứa giá trị trung vị chiều cao thành viên đội Sao La là \(\begin{array}{*{20}{l}}{\;\left[ {180;185} \right)}\end{array}\).

Nhóm chứa giá trị trung vị chiều cao thành viên đội Kim Ngưu là \(\begin{array}{*{20}{l}}{\;\left[ {185;190} \right)}\end{array}\).

Thực hành 1

Hãy trả lời câu hỏi ở Hoạt động mở đầu.

Phương pháp giải:

Tính số trung bình và số trung vị theo bảng tần số ghép nhóm rồi so sánh.

Lời giải chi tiết:

Ta có số liệu thống kê chiều cao thành viên của hai đội như sau:

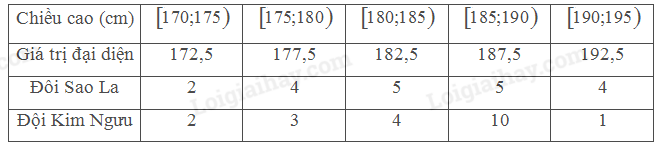
• Chiều cao trung bình của thành viên đội Sao La là:

\(\bar x = \frac{{2.172,5 + 4.177,5 + 5.182,5 + 5.187,5 + 4.192,5}}{{20}} = 183,75\left( {cm} \right)\)

Nhóm chứa số trung vị của đội Sao La là: \(\begin{array}{*{20}{l}}{\;\left[ {180;185} \right)}\end{array}\)

Ta có: \(n = 20;{n_m} = 5;C = 2 + 4 = 6;{u_m} = 180;{u_{m + 1}} = 185\)

Trung vị của chiều cao của thành viên đội Sao La là:

\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 180 + \frac{{\frac{{20}}{2} - 6}}{5}.\left( {185 - 180} \right) = 184\left( m \right)\)

• Chiều cao trung bình của thành viên đội Kim Ngưu là:

\(\bar x = \frac{{2.172,5 + 3.177,5 + 4.182,5 + 10.187,5 + 1.192,5}}{{20}} = 183,75\left( {cm} \right)\)

Nhóm chứa số trung vị của đội Kim Ngưu là: \(\begin{array}{*{20}{l}}{\;\left[ {185;190} \right)}\end{array}\)

Ta có: \(n = 20;{n_m} = 10;C = 2 + 3 + 4 = 9;{u_m} = 185;{u_{m + 1}} = 190\)

Trung vị của chiều cao của thành viên đội Kim Ngưu là:

\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 185 + \frac{{\frac{{20}}{2} - 9}}{{10}}.\left( {190 - 185} \right) = 185,5\left( m \right)\)

Vậy chiều cao trung bình của hai đội bằng nhau, số trung vị của đội Sao La nhỏ hơn số trung vị của đội Kim Ngưu.

Vận dụng 1

Trong một hội thao, thời gian chạy 200 m của một nhóm các vận động viên được ghi lại ở bảng sau: 

Dựa vào bảng số liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây?

Phương pháp giải:

Tính số trung vị theo bảng tần số ghép nhóm.

Lời giải chi tiết:

Số vận động viên tham gia là: \(n = 5 + 12 + 32 + 45 + 30 = 124\).

Gọi \({x_1};{x_2};...;{x_{124}}\) lần lượt là thời gian chạy của 124 vận động viên được xếp theo thứ tự không giảm.

Do \({x_1};...;{x_5} \in \begin{array}{*{20}{l}}{\left[ {21;21,5} \right)}\end{array};{x_6};...;{x_{17}} \in \begin{array}{*{20}{l}}{\left[ {21,5;22} \right)}\end{array};{x_{18}};...;{x_{49}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {22;22,5} \right)}\end{array}}\end{array};\)\({x_{50}};...;{x_{94}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {22,5;23} \right)}\end{array}}\end{array}}\end{array}\) nên trung vị của mẫu số liệu là: \(\frac{1}{2}\left( {{x_{62}} + {x_{63}}} \right) \in \begin{array}{*{20}{l}}{\left[ {22,5;23} \right)}\end{array}\)

Ta có: \(n = 124;{n_m} = 45;C = 5 + 12 + 32 = 49;{u_m} = 22,5;{u_{m + 1}} = 23\)

Trung vị của thời gian chạy của các vận động viên là:

\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 22,5 + \frac{{\frac{{124}}{2} - 49}}{{45}}.\left( {23 - 22,5} \right) \approx 22,64\)

Vậy ban tổ chức nên chọn các vận động viên có thời gian chạy không quá 22,64 giây