Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác (frac{{2pi
Hoạt động 1
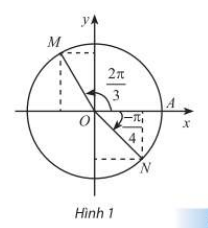
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
Phương pháp giải:
Dựa vào kiến thức đã học để xác định
Lời giải chi tiết:
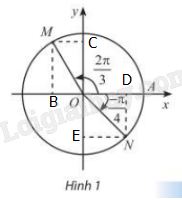
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy
D,E lần lượt là hình chiếu của N lên Ox, Oy
Ta có OM = ON = 1
\(\widehat {MOC} = \frac{{2\pi }}{3} - \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M \(\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
\(\widehat {NOD} = - \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = - \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = - \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.\)
Tọa độ của điểm N \(\left( { \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)\)
Thực hành
Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
Phương pháp giải:
Dựa vào kiến thức đã học ở phần trên để tính
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan 495^\circ = - 1\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo timdapan.com"







