Đề thi học kì 1 môn toán lớp 6 năm 2019 - 2020 phòng GDĐT Bình Tân

Câu 1  (2 điểm):

a) Tính : \(\left\{ {540:\left[ {79 - \left( {5.7 + 34} \right)} \right]} \right\}:9 + 8\)

b) Tìm \(x\) biết : \(1823 - \left( {9 + x} \right) = 1259\)

Câu 2 (1 điểm): Nhà ba bạn \(A,B,C\) cùng nằm trên một đường thẳng, nhà bạn \(B\) nằm giữa nhà hai bạn \(A\) và \(C.\) Khoảng cách từ nhà bạn \(A\) đến nhà bạn \(B\) là \(2km,\) khoảng cách từ nhà bạn \(B\) đến nhà bạn \(C\) là \(3km.\) Tính khoảng cách từ nhà bạn \(A\) đến nhà bạn \(C.\) 

Câu 3 (1 điểm): Học sinh khối \(6\) có \(195\) nam và \(117\) nữ tham gia lao động. Thầy phụ trách muốn chia ra thành các tổ sao cho số nam và nữ ở mỗi tổ đều bằng nhau. 

a) Hỏi có thể chia được nhiều nhất thành mấy tổ ?

b) Khi đó, mỗi tổ có bao nhiêu học sinh nam và bao nhiêu học sinh nữ ?

Câu 4 (1 điểm): Bác Hồ sinh năm \(\overline {1a9b} .\) Biết \(\overline {1a9b} \) chia hết cho \(2,5\) và \(9.\) Tìm năm sinh của Bác Hồ ?

Câu 5 (1 điểm): Mẹ cho An \(100\,000\) đồng để đi mua vở. Cửa hàng \(A\) bán với giá \(5000\) đồng/quyển vở. Cũng cùng loại vở đó nhưng cửa hàng \(B\) kế bên bán với giá \(6000\) đồng/quyển vở và có thêm chương trình khuyến mãi cứ mua \(5\) cuốn được tặng thêm \(1\) cuốn cùng loại miễn phí. Theo em, với \(100\,000\) đồng mà mẹ cho thì An nên mua vở ở cửa hàng nào để có được nhiều quyển vở hơn (kể cả hàng tặng) ? Vì sao ?

Câu 6 (3,5 điểm): Trên tia \(Ox\) lấy hai điểm \(A,B\) sao cho \(OA = 6cm,OB = 12cm.\)

a) Tính độ dài đoạn thẳng \(AB?\)

b) Điểm \(A\) có là trung điểm của đoạn thẳng \(OB\) không ? Vì sao ?

c) Gọi \(M\) là trung điểm của đoạn thẳng \(AB.\) Trên tia \(Bx\) lấy điểm \(N\) sao cho \(BN = 4cm\) và lấy điểm \(C\) sao cho \(N\) là trung điểm của \(BC.\) Tính độ dài đoạn thẳng \(MB\) và \(AC?\)

Câu 7 (0,5 điểm): Tổng của \(38\) số tự nhiên liên tiếp bằng \(2052\). Hãy tìm số nhỏ nhất trong \(38\) số đó.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu 1 (VD):

Phương pháp:

a) Áp dụng quy tắc về thứ tự thực hiện các phép tính khi biểu thức có dấu ngoặc : Tính các biểu thức trong ngoặc ( ), rồi đến ngoặc [ ] và cuối cùng là ngoặc { }.

Biểu thức không có dấu ngoặc : Tính nhân, chia trước; cộng, trừ sau.

b) Áp dụng quy tắc chuyển vế đổi dấu và quy tắc phá ngoặc để tìm giá trị của \(x.\)

Cách giải:

a)

\(\begin{array}{l}\left\{ {540:\left[ {79 - \left( {5.7 + 34} \right)} \right]} \right\}:9 + 8\\ = \left\{ {540:\left[ {79 - \left( {35 + 34} \right)} \right]} \right\}:9 + 8\\ = \left[ {540:\left( {79 - 69} \right)} \right]:9 + 8\\ = \left( {540:10} \right):9 + 8\\ = 54:9 + 8\\ = 6 + 8\\ = 14\end{array}\)

b) \(1823 - \left( {9 + x} \right) = 1259\)

\(\begin{array}{l}9 + x = 1823 - 1259\\9 + x = 564\\x = 564 - 9\\x = 555\end{array}\)  

Câu 2 (VD):

Phương pháp:

Vận dụng kiến thức về tính chất điểm nằm giữa hai điểm:

Nếu điểm \(M\) nằm giữa hai điểm \(A,B\) thì \(AM + MB = AB\).

Cách giải:

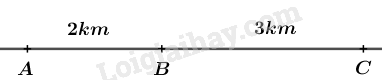
Ta có \(A,B,C\) cùng nằm trên một đường thẳng nên ba điểm thẳng hàng và \(B\) nằm giữa hai điểm \(A\) và \(C\) nên \(AB + BC = AC\)

Mà \(AB = 2km;\,AC = 3km\) nên \(AC = 2 + 3 = 5\left( {km} \right)\)

Vậy khoảng cách từ nhà bạn \(A\) đến nhà bạn \(C\) là \(5km.\)

Câu 3 (VD):

Học sinh khối \(6\) có \(195\) nam và \(117\) nữ tham gia lao động. Thầy phụ trách muốn chia ra thành các tổ sao cho số nam và nữ ở mỗi tổ đều bằng nhau.

Phương pháp:

a) Số tổ nhiều nhất chia được là ƯCLN(195; 117)

b) Tìm được số tổ ở câu a, từ đó tìm được số học sinh nam và nữ của mỗi tổ.

Cách giải:

a) Hỏi có thể chia được nhiều nhất thành mấy tổ ?

Gọi số tổ chia được nhiều nhất là \(a\left( {a \in {\mathbb{N}^*}} \right)\) thì ta có \(195 \vdots a\); \(117 \vdots a\) và \(a\) có giá trị lớn nhất hay \(a\) là ƯCLN(195, 117)

Ta có : \(195 = 3.5.13\) ;

\(117 = {3^2}.13\)

\( \Rightarrow \) ƯCLN\(\left( {195;117} \right) = 3.13 = 39\)

Vậy có thể chia được nhiều nhất thành \(39\) tổ.

b) Khi đó, mỗi tổ có bao nhiêu học sinh nam và bao nhiêu học sinh nữ ?

Khi đó mỗi tổ có số học sinh nam là :

\(195:39 = 5\) (học sinh)

Khi đó mỗi tổ có số học sinh nữ là :

\(117:39 = 3\) (học sinh)

Vậy mỗi tổ có \(5\) học sinh nam, \(3\) học sinh nữ.

Câu 4 (VD):

Phương pháp:

Nhẩm lại dấu hiệu chia hết của \(2,5,9\) và tìm giá trị của \(a,b.\)

- Một số chia hết cho \(2\) khi tận cùng của số đó bằng một trong các số \(0,2,4,6,8\)

- Một số chia hết cho \(5\) khi tận cùng của số đó bằng \(0\) hoặc \(5.\)

- Một số chia hết cho \(9\) khi tổng các chữ số của số đó cũng chia hết cho \(9\).

Cách giải:

Vì số \(\overline {1a9b} \) chia hết cho cả \(2\) và \(5\) nên tận cùng của số đó là chữ số \(0\) hay \(b = 0.\)

Số \(\overline {1a90} \) có tổng các chữ số bằng \(1 + a + 9 + 0 = 10 + a\)

Để tổng các chữ số chia hết cho \(9\) thì \(a = 8.\)

Vậy năm sinh của Bác Hồ là \(1890.\)

Câu 5 (VD):

Phương pháp:

- Tính số quyển vở An mua được nếu mua ở cửa hàng A : Lấy 100 000 đồng chia cho giá tiền của một quyển.

- Tính số quyển vở An mua được nếu mua ở cửa hàng B và số vở được tặng kèm.

- So sánh rồi trả lời câu hỏi của bài toán.

Cách giải:

Nếu mua vở ở cửa hàng \(A\) thì An mua được số quyển vở là :

\(100\,000:5000 = 20\) (quyển vở)

Nếu mua ở cửa hàng \(B\) thì An mua được số quyển vở (chưa tính vở được tặng kèm) là :

\(100\,000:6000 = 16\) (quyển vở) thừa \(4000\) đồng

Ta có : \(16:5 = 3\) dư \(1\) nên An được tặng \(3\) quyển vở ở cửa hàng \(B\).

Vậy nếu mua ở cửa hàng \(B\) thì An mua được \(16 + 3 = 19\) (quyển vở)

Với 100 000 đồng mà mẹ cho thì An nên mua vở ở cửa hàng \(A\) để có được nhiều quyển vở hơn.

Câu 6 (VD):

Phương pháp:

- Áp dụng kiến thức : Điểm M nằm giữa \(A\) và \(B\) thì \(AM + MB = AB\)

- Trung điểm N của đoạn thẳng \(AB\) khi \(N\) nằm giữa \(A\) và \(B\) đồng thời \(NA = NB = \dfrac{{AB}}{2}\) 

Cách giải:

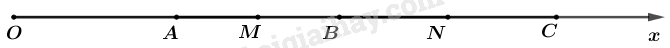
a) Tính độ dài đoạn thẳng \(AB?\)

Do \(A,B\) cùng nằm trên tia \(Ox\) nên ba điểm \(O,A,B\) thẳng hàng.

Mà \(OA < OB\)(\(6cm < 12cm\)) nên \(A\) nằm giữa hai điểm \(O\) và \(B\).

Ta có : \(OA + AB = OB\)

Mà \(OA = 6cm;\,OB = 12cm\) nên thay số vào biểu thức trên ta được :

\(\begin{array}{l}6 + AB = 12\\AB = 12 - 6 = 6\left( {cm} \right)\end{array}\)

b) Điểm \(A\) có là trung điểm của đoạn thẳng \(OB\) không ? Vì sao ?

Ta có \(A\) là điểm nằm giữa \(O\) và \(B\) (câu a)

Và \(OA = AB = 6cm\) nên \(A\) là trung điểm của đoạn thẳng \(OB.\)

c) Gọi \(M\) là trung điểm của đoạn thẳng \(AB.\) Trên tia \(Bx\) lấy điểm \(N\) sao cho \(BN = 4cm\) và lấy điểm \(C\) sao cho \(N\) là trung điểm của \(BC.\) Tính độ dài đoạn thẳng \(MB\) và \(AC?\)

+) Vì \(M\) là trung điểm của \(AB\) và \(AB = 6cm\) (câu a) nên \(MA = MB = \dfrac{{AB}}{2} = \dfrac{6}{2} = 3\left( {cm} \right)\)

+) Vì \(BN = 4cm\) và \(N\) là trung điểm của \(BC\) (cách vẽ) nên

\(\begin{array}{l}BN = NC = \dfrac{{BC}}{2}\\ \Rightarrow BC = 2 \times BN = 2 \times 4cm = 8cm\end{array}\)

Ta có : \(C\) thuộc tia \(Bx.\)

Theo câu a, điểm \(A\) nằm giữa \(O,B\) hay \(A\) nằm ở tia đối của tia \(Bx\)

\(A\) và \(C\) nằm trên hai tia đối nhau gốc \(B\) nên \(B\) là điểm nằm giữa hai điểm \(A,C\).

Ta có: \(AB + BC = AC\)

Mà \(AB = 6cm;\,BC = 8cm\) nên \(AC = 6 + 8 = 14\left( {cm} \right)\).

Câu 7 (VD):

Phương pháp:

Áp dụng kiến thức về dãy số :

- Số số hạng = (số cuối – số đầu) : Khoảng cách + 1

- Tổng = (số cuối + số đầu) × số số hạng : 2.

Cách giải: 

Dãy số đã cho có \(38\) số. Giả sử các số được viết theo thứ tự từ bé đến lớn. Số đầu của dãy số đó là số có giá trị nhỏ nhất.

38 số lẻ liên tiếp thì số cuối cách số đầu số giá trị là : \(\left( {38 - 1} \right) \times 2 = 74\) (đơn vị)

Tổng của các số đó bằng : (số đầu + số cuối) × Số số hạng : 2

Hay tổng của 38 số đó bằng : (số đầu + số đầu + 74) × 38 : 2 =2052

Vậy số nhỏ nhất của dãy số đó là : \(\left( {2052 \times 2:38 - 74} \right):2 = 17\)