Đề kiểm tra 45 phút chương 2 phần Hình học 6 - Đề số 2

Đề bài

Câu 1. (3 điểm) Điền vào chỗ trống :

Tia phân giác của góc là ………….

Câu 2. (3 điểm) Cho hai tia \(Oy,Oz\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox.\)

Biết \(\widehat {xOy} = 30^\circ ,\widehat {xOz} = 100^\circ .\) Gọi \(Ot\) là tia phân giác của \(\widehat {xOy},Ot'\) là tia phân giác của \(\widehat {yOz}.\) Tính \(\widehat {tOt'}.\)

Câu 3. (4 điểm) Vẽ \(\Delta ABC\) biết \(AB = 5cm,\,BC = 4cm,\,CA = 3cm.\)Vẽ trung điểm \(I\) của \(AB.\)

Vẽ đoạn thẳng \(CI.\) So sánh các đoạn thẳng \(CI,AI,BI.\)

LG câu 1

Phương pháp giải :

Nhớ lại định nghĩa tia phân giác đã học.

Cách giải

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

LG câu 2

Phương pháp giải :

+) Trên nửa mặt phẳng bờ chứa tia \(Ox\) có hai tia \(Oy, Oz\) mà \(\widehat{xOy}< \widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

+) Sử dụng công thức cộng góc

+) Sử dụng: Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2\)

Cách giải

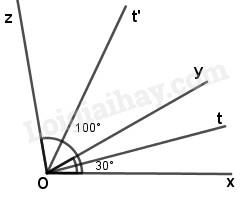
Vì hai tia \(Oy, Oz\) cùng nằm trên nửa mặt phẳng bờ chứa tia \(Ox\) mà 

\(\widehat{ xOy}\)<  \(\widehat{ xOz}\) \((30^0<100^0)\) nên tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

Do đó  \(\widehat{ xOy}\)+ \(\widehat{ yOz}\)= \(\widehat{ xOz}\)  

Suy ra  \(\widehat{ yOz}=\widehat{ xOz}-\widehat{ xOy}\)\(= 100^0-30^0=70^0\) 

Ta có tia \(Ot\) là tia phân giác của góc \(xOy\) nên: \(\widehat {xOt} = \widehat {tOy} \)\(= \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{30}^0}}}{2} = {15^0}\)

Tia \(Ot’\) là tia phân giác của góc \(yOz\) nên: \(\widehat {yOt’} = \widehat {t’Oz} = \dfrac{{\widehat {yOz}}}{2} \)\(= \dfrac{{{{70}^0}}}{2} = {35^0}\)

Vì tia \(Oy\) nằm giữa hai tia \(Ox,Oz\) mà tia \(Ot’\) là tia phân giác góc \(zOy\), tia \(Ot\) là tia phân giác góc \(xOy\) nên \(Ot\) và \(Ot’\) nằm trên hai nửa mặt phẳng đối nhau bờ là tia \(Oy\). Do đó tia \(Oy\) nằm giữa hai tia \(Ot, Ot’\), suy ra: 

\(\widehat{tOt’}\) =\(\widehat{tOy}\) + \(\widehat{yOt’}\) \( = {15^0} + {35^0} = {50^0}\)

LG câu 3

Phương pháp giải :

- Vẽ hình theo đề bài.

- Trung điểm của một đoạn thẳng là điểm nằm chính giữa đoạn thẳng đó và chia đoạn thẳng đó thành hai phần bằng nhau.

Cách giải

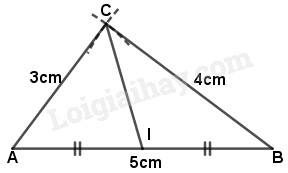
• Vẽ tam giác \(ABC\) :

- Vẽ đoạn thẳng \(AB = 5 cm.\)

- Vẽ cung tròn tâm \(A\), bán kính \(3cm\).

- Vẽ cung tròn tâm \(B\), bán kính \(4 cm\).

- Lấy một giao điểm của hai cung trên, gọi giao điểm đó là \(C.\)

- Vẽ đoạn thẳng \(AB, AC\), ta có tam giác \(ABC.\)

• Trên đoạn \(AB\) lấy điểm \(I\) sao cho \(IA=IB=\dfrac{AB}{2}\).

• Nối \(IC\)

• Đo các đoạn thẳng \(IC, AI, BI\) có trong hình ta có : \(IC=2,5cm\); \(IA=2,5cm\); \(IB=2,5cm\)

Vậy ba đoạn thẳng \(IC, AI, BI\) bằng nhau.