Đề kiểm tra 45 phút chương 2 phần Hình học 6 - Đề số 1

Đề bài

Câu 1. (3 điểm) Điền vào chỗ trống :

Góc là ………..

Câu 2. (3 điểm) Vẽ hai góc kề bù \(xOy,yOx',\) biết \(\widehat {xOy} = 60^\circ .\) Gọi \(Ot\) là tia phân giác của góc \(xOy,Ot'\) là tia phân giác của góc \(x'Oy.\) Tính \(\widehat {tOt'}.\)

Câu 3. (4 điểm) Vẽ \(\Delta ABC\)có ba cạnh là \(AB = 4cm,\,AC = 3cm,\,BC = 2,5cm.\) Sắp xếp các góc của tam giác đó theo thứ tự tăng dần.

LG câu 1

Phương pháp giải :

Vận dụng khái niệm góc đã học rồi điền vào chỗ trống.

Cách giải

Góc là hình gồm hai tia chung gốc.

LG câu 2

Phương pháp giải :

+ Vẽ hình

+ Hai góc kề bù là hai góc kề nhau và có tổng số đo bằng 180 độ.

+ Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2\)

 Cách giải

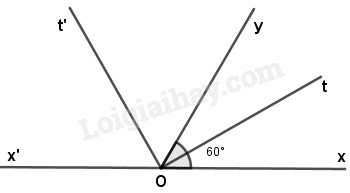
Vì \(Ot\) là tia phân giác của góc \(xOy\) nên:

\(\widehat{xOt} = \widehat {tOy} \)\(= \dfrac{1}2\widehat{xOy}\) \(=30^\circ\)

Hai góc \(x'Oy\) và \(xOy\) là hai góc kề bù nên :

\(\widehat {x'Oy} + \widehat {xOy} = {180^\circ}\)

Từ đó \(\widehat {x'Oy} = {180^\circ}- \widehat {xOy} \)\(= {180^\circ} - {60^\circ} = {120^\circ} \) 

Vì \(Ot’\) là tia phân giác của góc \(x’Oy\) nên:

\(\widehat{x’Ot’} = \widehat {t’Oy} \)\(= \dfrac{1}2\widehat{x’Oy}\) \(=60^\circ\)

Có tia \(Oy\) nằm giữa hai tia \(Ot\) và \(Ot’\) nên \(\widehat {tOy} + \widehat {yOt'} = \widehat {tOt'}\)\( \Rightarrow \widehat {tOt'} = 30^\circ  + 60^\circ  = 90^\circ .\)

LG câu 3

Phương pháp giải :

- Dùng thước thẳng và compa để vẽ hình 

- Dùng thước đo độ để đo các góc của tam giác \(ABC\)

- Sắp xếp các góc theo thứ tự tăng dần.

Cách giải

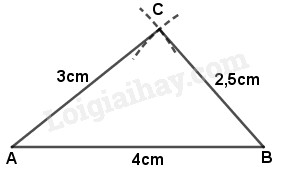
- Vẽ đoạn thẳng \(AB = 4 cm.\)

- Vẽ cung tròn tâm \(A\), bán kính \(3cm\).

- Vẽ cung tròn tâm \(B\), bán kính \(2,5 cm\).

- Lấy một giao điểm của hai cung trên, gọi giao điểm đó là \(C.\)

- Vẽ đoạn thẳng \(AB, AC\), ta có tam giác \(ABC.\)

- Đo các góc của tam giác \(ABC\) ta được : \(\widehat A \approx {38^\circ 37'};\,\widehat B \approx {48^\circ31'};\,\widehat C \approx {92^\circ52’}\).

Vậy \(\widehat A < \widehat B < \widehat C\)