Giải câu hỏi trắc nghiệm trang 74, 75 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Câu 1

Trong không gian, khẳng định nào sau đây đúng?

A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

Phương pháp giải:

Sử dụng kiến thức về tính chất hai đường thẳng vuông góc: Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

Lời giải chi tiết:

Khẳng định đúng: Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

Chọn A

---

Câu 2

Khẳng định nào sau đây sai?

A. Nếu đường thẳng \(d \bot \left( \alpha  \right)\) thì d vuông góc với hai đường thẳng trong \(\left( \alpha  \right)\).

B. Nếu đường thẳng d vuông góc với hai đường thẳng trong \(\left( \alpha  \right)\) thì \(d \bot \left( \alpha  \right)\).

C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( \alpha  \right)\) thì d vuông góc với bất kì đường thẳng nào nằm trong \(\left( \alpha  \right)\).

D. Nếu \(d \bot \left( \alpha  \right)\) và đường thẳng a//\(\left( \alpha  \right)\) thì \(d \bot a\).

Phương pháp giải:

Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong \(\left( \alpha  \right)\) thì \(d \bot \left( \alpha  \right)\).

Lời giải chi tiết:

Khẳng định sai: Nếu đường thẳng d vuông góc với hai đường thẳng trong \(\left( \alpha  \right)\) thì \(d \bot \left( \alpha  \right)\).

Chọn B.

---

Câu 3

Cho tứ diện ABCD. Vẽ \(AH \bot \left( {BCD} \right)\). Biết H là trực tâm tam giác BCD. Khẳng định nào sau đây đúng?

A. \(AB = CD\)

B. \(AC = BD\)

C. \(AB \bot CD\)

D. \(CD \bot BD\)

Phương pháp giải:

Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng: Nếu đường thẳng d vuông góc với mặt phẳng \(\left( \alpha  \right)\) thì d vuông góc với bất kì đường thẳng nào nằm trong \(\left( \alpha  \right)\).

Lời giải chi tiết:

Vì \(AH \bot \left( {BCD} \right) \Rightarrow AH \bot CD\)

Vì H là trực tâm tam giác BCD nên \(BH \bot CD\)

Ta có: \(AH \bot CD\), \(BH \bot CD\), BH và AH cắt nhau tại H và nằm trong mặt phẳng (BAH).

Do đó, \(CD \bot \left( {ABH} \right) \Rightarrow CD \bot AB\)

Chọn C

---

Câu 4

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Gọi E, F lần lượt là hình chiếu của A lên SB, SD. Khẳng định nào sau đây sai?

A. \(SC \bot EF\)

B. \(SC \bot AE\)

C. \(SC \bot AF\)

D. \(SC \bot BC\)

Phương pháp giải:

+ Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

+ Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia. 

Lời giải chi tiết:

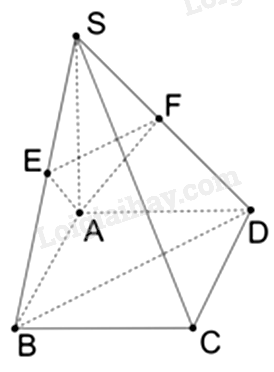
+ Vì ABCD là hình vuông nên \(AB \bot BC\).

Mà \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)

Do đó, \(BC \bot \left( {SAB} \right)\). Lại có: \(BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)

Mà SB là giao tuyến của (SBC) và (SAB), \(AE \bot SB\) nên \(EA \bot \left( {SBC} \right) \Rightarrow AE \bot SC\)

Đáp án B đúng

+ Vì ABCD là hình vuông nên \(AD \bot DC\).

Mà \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)

Do đó, \(DC \bot \left( {SAD} \right)\). Lại có: \(DC \subset \left( {SDC} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\)

Mà SD là giao tuyến của (SDC) và (SAD), \(AF \bot SD\) nên \(FA \bot \left( {SDC} \right) \Rightarrow AF \bot SC\)

Đáp án C đúng

+ Vì \(AE \bot SC,AF \bot SC\) nên \(SC \bot \left( {AEF} \right)\). Do đó, \(SC \bot EF\)

Đáp án A đúng

Vì \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\). Do đó, tam giác SBC vuông tại B. Do đó, SC không thể vuông góc với BC.

Đáp án D sai.

Chọn D

---

Câu 5

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên \(SA = 2a\) và vuông góc với mặt phẳng đáy. Gọi \(\alpha \) là góc tạo bởi đường thẳng SC và mặt phẳng đáy. Khẳng định nào sau đây đúng?

A. \(\alpha  = {60^0}\)

B. \(\alpha  = {75^0}\)

C. \(\tan \alpha  = 1\)

D. \(\tan \alpha  = \sqrt 2 \)

Phương pháp giải:

Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:

+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).

+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P). 

Lời giải chi tiết:

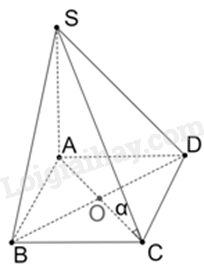
Vì \(SA \bot \left( {ABCD} \right)\) nên A là hình chiếu của S trên mặt phẳng (ABCD).

Do đó, \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)

Vì ABCD là hình vuông nên \(\widehat {ABC} = {90^0}\)

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có: \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2 \)

Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC\) nên tam giác SAC vuông tại A.

Suy ra: \(\tan \alpha  = \frac{{SA}}{{AC}} = \frac{{2a}}{{a\sqrt 2 }} = \sqrt 2 \)

Chọn D

---

Câu 6

Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?

A. Góc giữa AC và (BCD) là góc ACB.

B. Góc giữa AD và (ABC) là góc ADB.

C. Góc giữa AC và (ABD) là góc ACB.

D. Góc giữa CD và (ABD) là góc CBD.

Phương pháp giải:

Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:

+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).

+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P). 

Lời giải chi tiết:

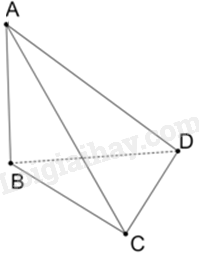
Vì \(AB \bot BC,AB \bot BD \Rightarrow AB \bot \left( {BCD} \right)\)

Do đó, B là hình chiếu của A trên mặt phẳng BCD.

Suy ra, \(\left( {AC,\left( {BCD} \right)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\)

Chọn A.

---

Câu 7

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và \(AB = a\sqrt 2 \). Biết \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Góc giữa hai mặt phẳng (SBC) và (ABC) bằng

A. \({30^0}\)

B. \({45^0}\)

C. \({60^0}\)

D. \({90^0}\)

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng. 

Lời giải chi tiết:

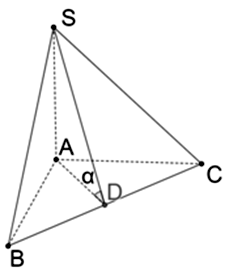
Trong mặt phẳng ABC, kẻ \(AD \bot BC\left( {D \in BC} \right)\)

Mà \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(AD \bot BC\), do đó, \(BC \bot \left( {SAD} \right) \Rightarrow BC \bot SD\)

Vì \(BC \bot SD,AD \bot BC,AD \subset \left( {ABC} \right),SD \subset \left( {SBC} \right)\) và BC là giao tuyến của (SBC) và (ABC). Do đó, \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {SD,AD} \right) = \widehat {SDA}\)

Tam giác ABC vuông cân tại A nên \(\widehat {ABC} = {45^0}\)

Tam giác ADB vuông tại D nên \(AD = AB.\sin \widehat {ABC} = a\sqrt 2 .\sin {45^o} = a\)

Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AD\). Do đó, tam giác SAD vuông tại A.

Mà \(SA = AD\left( { = a} \right)\) nên tam giác SAD vuông cân tại A. Do đó, \(\widehat {SDA} = {45^0}\)

Chọn B

---

Câu 8

Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì

A. Song song với nhau.

B. Trùng nhau.

C. Không song song với nhau.

D. Hoặc song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.

Phương pháp giải:

Sử dụng kiến thức về hai mặt phẳng vuông góc: Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì hoặc song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.

Lời giải chi tiết:

Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì hoặc song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.

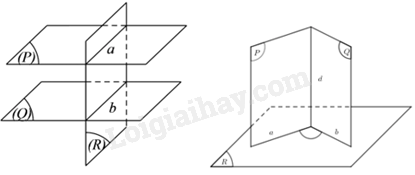
Chọn D

---

Câu 9

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A’BC) bằng

A. \(\frac{a}{{\sqrt 2 }}\)

B. \(\frac{{a\sqrt 6 }}{4}\)

C. \(\frac{{a\sqrt 3 }}{{\sqrt 7 }}\)

D. \(\frac{{a\sqrt 3 }}{4}\)

Phương pháp giải:

Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)). 

Lời giải chi tiết:

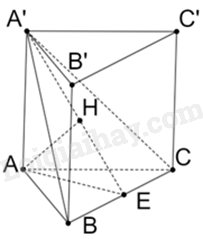
Gọi E là trung điểm của BC. Vì tam giác ABC đều nên AE là đường trung tuyến đồng thời là đường cao. Do đó, \(AE \bot BC\)

Mà \(A'A \bot \left( {ABC} \right) \Rightarrow A'A \bot BC\). Do đó, \(BC \bot \left( {A'AE} \right)\).

Trong mặt phẳng (A’AE), kẻ \(AH \bot A'E\left( {H \in A'E} \right) \Rightarrow AH \bot BC\)

Vì \(AH \bot BC,AH \bot A'E \Rightarrow AH \bot \left( {A'BC} \right)\). Do đó, H là hình chiếu của A trên mặt phẳng (A’BC) hay AH là khoảng cách từ A đến mặt phẳng (A’BC)

Vì tam giác ABC đều nên \(AE = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)

Vì \(A'A \bot \left( {ABC} \right) \Rightarrow A'A \bot EA\). Do đó, tam giác A’EA vuông tại A.

Suy ra: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{E^2}}} + \frac{1}{{A'{A^2}}} = \frac{4}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AH = \frac{{a\sqrt 3 }}{{\sqrt 7 }}\)

Chọn C

---

Câu 10

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = 2a,BC = a\), mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC.

A. \(\frac{{a\sqrt {30} }}{{10}}\)

B. \(\frac{{a\sqrt 3 }}{2}\)

C. \(\frac{{a\sqrt {15} }}{5}\)

D. a

Phương pháp giải:

Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường thẳng đến mặt phẳng song song với nó và chứa đường thẳng còn lại. 

Lời giải chi tiết:

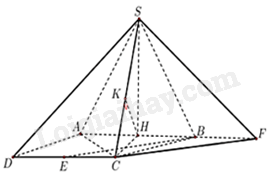
Gọi H là trung điểm của AB. Vì tam giác ABS đều nên SH là đường trung tuyến đồng thời là đường cao của tam giác.

Vì \(\left( {SAB} \right) \bot \left( {ABCD} \right),SH \bot AB,SH \subset \left( {SAB} \right)\) và AB là giao tuyến của hai mặt phẳng (SAB) và (ABCD) nên \(SH \bot \left( {ABCD} \right)\)

Gọi F đối xứng với H qua B nên B là trung điểm của FH hay \(HB \) \( = BF\)

Chứng minh được tứ giác BECF là hình bình hành. Do đó, BE//CF

Do đó, \(d\left( {BE,CS} \right) \) \( = d\left( {BE,\left( {SCF} \right)} \right) \) \( = d\left( {B,\left( {SCF} \right)} \right) \) \( = \frac{1}{2}d\left( {H,\left( {SCF} \right)} \right)\)

Chứng minh được tứ giác HBCE là hình vuông cạnh a nên \(CH \) \( = BE \) \( = CF \) \( = a\sqrt 2 \)

Mà \(C{H^2} + C{F^2} \) \( = H{F^2}\left( { \) \( = 4{a^2}} \right)\) nên tam giác HCF vuông cân tại C.

Vì \(CF \bot HC,CF \bot SH \Rightarrow CF \bot \left( {SHC} \right) \Rightarrow \left( {SCF} \right) \bot \left( {SHC} \right)\)

Trong (SHC), kẻ \(HK \bot SC \Rightarrow HK \bot \left( {SCF} \right)\).

Suy ra \(d\left( {H,\left( {SCF} \right)} \right) \) \( = HK \Rightarrow d\left( {BE,SC} \right) \) \( = \frac{1}{2}HK\)

Vì SH là đường cao trong tam giác đều SAB nên \(SH \) \( = \frac{{BA\sqrt 3 }}{2} \) \( = \frac{{2a\sqrt 3 }}{2} \) \( = a\sqrt 3 \)

Tam giác SHC vuông tại H, đường cao HK có: \(\frac{1}{{H{K^2}}} \) \( = \frac{1}{{C{H^2}}} + \frac{1}{{S{H^2}}} \) \( = \frac{1}{{2{a^2}}} + \frac{1}{{3{a^2}}} \) \( = \frac{5}{{6{a^2}}} \Rightarrow HK \) \( = \frac{{a\sqrt {30} }}{5} \Rightarrow d\left( {BE,SC} \right) \) \( = \frac{1}{2}HK \) \( = \frac{{a\sqrt {30} }}{{10}}\)

Chọn A

---

Câu 11

Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = 2a,AD = a\). Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng \({45^0}\). Khi đó thể tích khối chóp S.ABCD là

A. \(\frac{{\sqrt 3 }}{3}{a^3}\)

B. \(\frac{1}{3}{a^3}\)

C. \(2{a^3}\)

D. \(\frac{2}{3}{a^3}\)

Phương pháp giải:

+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.

+ Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)

Lời giải chi tiết:

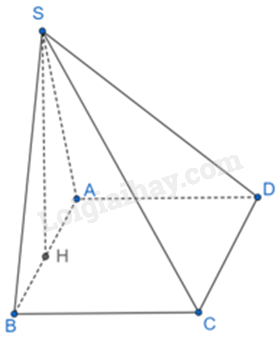
Gọi H là trung điểm của AB. Vì tam giác SAB cân tại S nên SH là đường trung tuyến đồng thời là đường cao. Do đó, \(SH \bot AB\)

Vì \(\left( {SAB} \right) \bot \left( {ABCD} \right),SH \bot AB,SH \subset \left( {SAB} \right)\), AB là giao tuyến của (SAB) và (ABCD). Do đó, \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BC\)

Vì ABCD là hình chữ nhật nên \(BC \bot AB\)

Mà \(SH \bot BC\), SH và AB cắt nhau tại H và nằm trong mặt phẳng SAB nên \(BC \bot \left( {SAB} \right)\)

Lại có: \(SB \subset \left( {SAB} \right) \Rightarrow BC \bot SB\)

Ta có: \(BC \bot SB,AB \bot BC,SB \subset \left( {SBC} \right),AB \subset \left( {ABCD} \right)\), BC là giao tuyến của 2 mặt phẳng (SBC) và (ABCD). Do đó, \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \left( {AB,SB} \right) = \widehat {SBA} = {45^0}\)

Vì \(SH \bot AB \Rightarrow \widehat {SHB} = {90^0}\). Mà \(\widehat {SBA} = {45^0}\) nên tam giác SHB vuông cân tại H.

Do đó, \(SH = HB = \frac{1}{2}AB = a\)

Thể tích khối chóp S. ABCD là: \(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}SH.AB.AD = \frac{1}{3}.a.a.2a = \frac{{2{a^3}}}{3}\)

Chọn D

---

Câu 12

Cho khối chóp S.ABCD có đáy là hình chữ nhật \(AB = a,AD = a\sqrt 3 \), SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc \({30^0}\). Tính thể tích V của khối chóp đã cho.

A. \(V = \frac{{2{a^3}\sqrt 6 }}{3}\)

B. \(V = \frac{{{a^3}\sqrt 6 }}{3}\)

C. \(V = 2\sqrt 6 {a^3}\)

D. \(V = \frac{{4{a^3}}}{3}\)

Phương pháp giải:

- Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:

+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).

+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).

- Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)

Lời giải chi tiết:

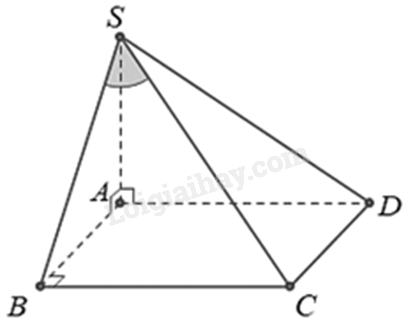
Vì \(SA \bot \left( {ABCD} \right),BC,AB \subset \left( {ABCD} \right) \Rightarrow SA \bot BC,SA \bot AB\) .

Ta có: \(SA \bot BC,AB \bot BC\) (do ABCD là hình chữ nhật), SA và AB cắt nhau tại A trong mặt phẳng (SAB) nên \(BC \bot \left( {SAB} \right) \Rightarrow \) B là hình chiếu của C trên mặt phẳng (SAB).

Do đó, \(\left( {SC,\left( {SAB} \right)} \right) = \left( {SC,SB} \right) = \widehat {CSB} = {30^0}\)

Vì \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\). Do đó, tam giác SBC vuông tại B.

Suy ra: \(SB = \frac{{BC}}{{\tan \widehat {BSC}}} = \frac{{a\sqrt 3 }}{{\frac{{\sqrt 3 }}{3}}} = 3a\)

Tam giác SAB vuông tại A nên ta có: \(SA = \sqrt {S{B^2} - A{B^2}}  = \sqrt {{{\left( {3a} \right)}^2} - {a^2}}  = 2a\sqrt 2 \) (Định lí Pythagore)

Thể tích khối chóp S. ABCD là: \({V_{S.ABCD}} = \frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{3}.2a\sqrt 2 .a.a\sqrt 3  = \frac{{2{a^3}\sqrt 6 }}{3}\)

Chọn A

---

Câu 13

Cho lăng trụ đứng ABC.A’B’C’ có đáy tam giác ABC vuông tại B, \(AB = 2a,BC = a,AA' = 2a\sqrt 3 \). Thể tích khối lăng trụ ABC.A’B’C’ là

A. \(4{a^3}\sqrt 3 \)

B. \(2{a^3}\sqrt 3 \)

C. \(\frac{{2{a^3}\sqrt 3 }}{3}\)

D. \(\frac{{4{a^3}\sqrt 3 }}{3}\)

Phương pháp giải:

Sử dụng kiến thức về thể tích khối lăng trụ: Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao: \(V = S.h\)

Lời giải chi tiết:

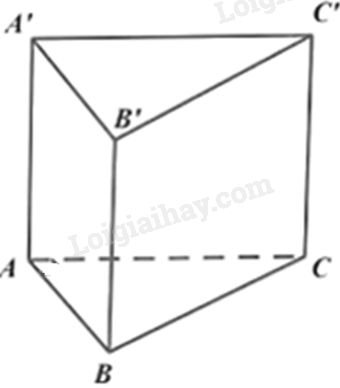
Thể tích khối lăng trụ ABC.A’B’C’ là: \(V = AA'.{S_{ABC}} = \frac{1}{2}AA'.AB.BC = \frac{1}{2}2a\sqrt 3 .a.2a = 2{a^3}\sqrt 3 \)

Chọn B

---

Câu 14

Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’. \({V_1}\) là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng?

A. \(V = 6{V_1}\)

B. \(V = 4{V_1}\)

C. \(V = 3{V_1}\)

D. \(V = 2{V_1}\)

Phương pháp giải:

+ Sử dụng kiến thức về thể tích hình lập phương: Thể tích hình lập phương bằng độ dài cạnh bên nhân với diện tích đáy.

+ Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)

Lời giải chi tiết:

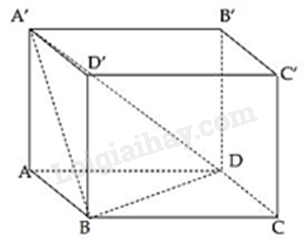
Thể tích của hình lập phương ABCD.A’B’C’D’ là: \(V = {S_{ABCD}}.AA'\)

Thể tích của tứ diện A’ABD là: \(V = \frac{1}{3}{S_{ABD}}.AA' = \frac{1}{3}.\frac{1}{2}{S_{ABCD}}.AA'\)

Do đó, \(V = 6{V_1}\)

Chọn A