Giải bài tập 5 trang 43 SGK Toán 12 tập 1 - Cánh diều

Đề bài

khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau:

a,\(y = 2{x^3} - 3x + 1\)

b,\(y =  - {x^3} + 3x - 1\)

c, \( y = {\left( {x - 2} \right)^3} + 4\)

d,\(y =  - {x^3} + 3{x^2} - 1\)

e, \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1\)

g,\( y =  - {x^3} - 3x\)

Lời giải chi tiết

a,\(y = 2{x^3} - 3x + 1\)

 \(y' = 6{x^2} - 3;y' = 0 =  > x =  \pm \sqrt {\frac{1}{2}} \)

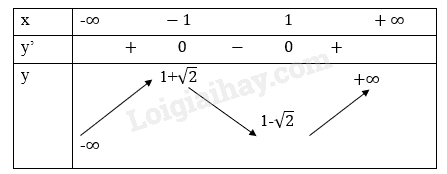
Đồ thị hàm số 

b, \(y =  - {x^3} + 3x - 1\)

\(y' =  - 3{x^2} + 3;y' = 0 =  > x =  \pm 1\)

Bảng biến thiên

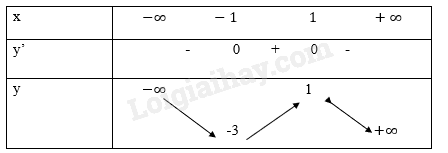
Đồ thị hàm số

c,\(y = {\left( {x - 2} \right)^3} + 4\)

 \(y' = 3{\left( {x - 2} \right)^2}\), y’=0 \( =  > {\left( {x\;-\;2} \right)^2} = 0 =  > x - 2 = 0 =  > x = 2\)

 Bảng biến thiên

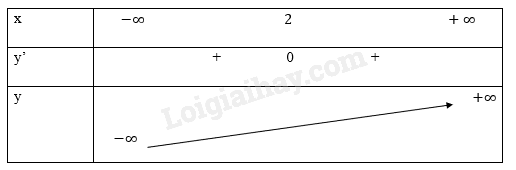
Đồ thị hàm số:  

d, \(y =  - {x^3} + 3{x^2} - 3x + 2\)

\(y' =  - 3{x^2} + 6x - 3,\;y' = 0 =  > x = 1\)

Bảng biến thiên:

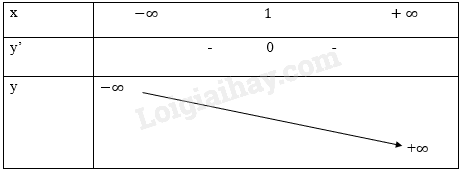
Đồ thị hàm số

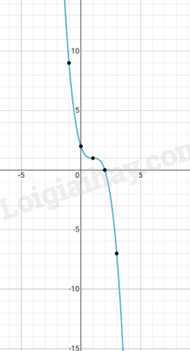
e,\(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1 =  > y' = {x^2} + 2x + 2\)

y’ = 0 => vô nghiệm

g,\(y =  - {x^3} - 3x =  > y' =  - 3{x^2} - 3,y' = 0\)

=> x vô nghiệm