Giải bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Sử dụng ý nghĩa hình học của tích phân, tính: a) \(\int\limits_1^2 {\left( {2x + 1} \right)dx} \); b) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} \).
Đề bài
Sử dụng ý nghĩa hình học của tích phân, tính:
a) \(\int\limits_1^2 {\left( {2x + 1} \right)dx} \);
b) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về ý nghĩa hình học của tích phân để tính: Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b], thì tích phân \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\). Vậy \(S = \int\limits_a^b {f\left( x \right)dx} \).
Lời giải chi tiết
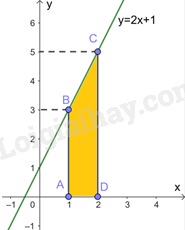
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 5\) và đường cao \(AD = 1\).
Do đó, \(\int\limits_1^2 {\left( {2x + 1} \right)dx} = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 5} \right).1 = 4\)
b) Ta có \(y = \sqrt {9 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.
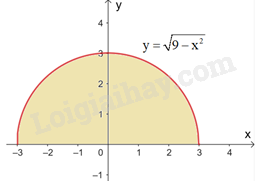
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} = \frac{9}{2}\pi \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức timdapan.com"







