Bài 9 trang 200 SBT hình học 11

Đề bài

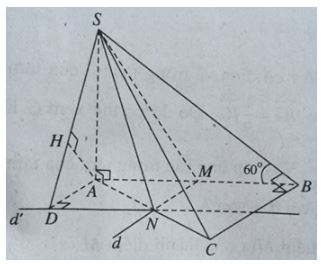
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABC). Gọi M là trung điểm của AB, mặt phẳng qua SM song song với BC cắt AC tại N. Biết góc tạo bởi (SBC) và (ABC) là 60^o. Tìm khoảng cách giữa hai đường thẳng AB và SN.

Lời giải chi tiết

Nhận xét

Gọi (α) là mặt phẳng qua SM và song song với AB.

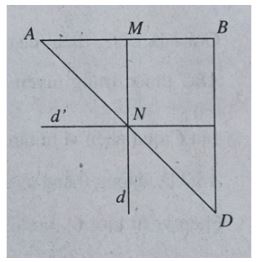
Ta có BC // (α) và (ABC) là mặt phẳng chứa BC nên (ABC) sẽ cắt (α) theo giao tuyến d đi qua M và song song với BC, d cắt AC tại N.

Ta có (α) chính là mặt phẳng (SMN). Vì M là trung điểm AB nên N là trung điểm AC.

+ Xác định khoảng cách.

Qua N kẻ đường thẳng d’ song song với AB.

Gọi (P) là mặt phẳng đi qua SN và d’.

Ta có: AB // (P).

Khi đó: d(AB, SN) = d(A, (P)).

Dựng AD ⊥ d’, ta có AB // (SDN). Kẻ AH vuông góc với SD, ta có AH ⊥ (SDN) nên:

d(AB, SN) = d(A, (SND)) = AH.

Trong tam giác SAD, ta có

 \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{D^2}}}\left( 1 \right)\)

Trong tam giác SAB, ta có SA = AB.tan60^o = 2a√3 và AD = MN = BC/2 = a.

Thế vào (1), ta được \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{12{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{{13}}{{12{a^2}}}\) \( \Rightarrow AH = \dfrac{{2a\sqrt {39} }}{{13}}\).