Giải bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ 45m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc 20 về phía tây bắc (hình 2). Tính tốc độ của gió
Đề bài
Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ \(45\)m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc \(20^\circ \) về phía tây bắc (hình 2). Tính tốc độ của gió
Phương pháp giải - Xem chi tiết
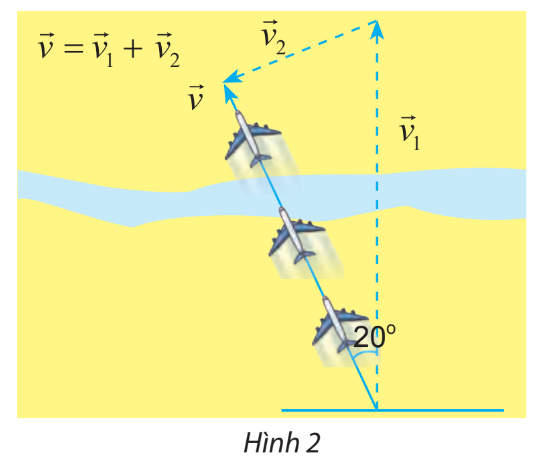
Bước 1: Dựa vào hình 2 xác định các vectơ tương ứng với vận tốc của máy bay, vận tốc so với mặt đất
Bước 2: Dựa vào mối liên hệ giữa các vectơ đã cho \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \) xác định vectơ tương ứng với vận tốc gió
Bước 3: Áp dụng định lý cosin tìm tốc độ của gió
Lời giải chi tiết
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)
+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)
Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)
Áp dụng định lý cosin ta có:
\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)
\( = \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)
Vậy tốc độ của gió gần bằng 16 m/s
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo timdapan.com"







