Giải bài 4 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho
Đề bài
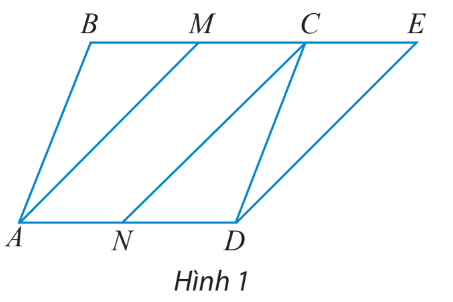
Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho \(\overrightarrow {CE} = \overrightarrow {AN} \) (hình 1)
a) Tìm tổng của các vectơ:
\(\overrightarrow {NC} \) và \(\overrightarrow {MC} \); \(\overrightarrow {AM} \) và \(\overrightarrow {CD} \); \(\overrightarrow {AD} \) và \(\overrightarrow {NC} \)
b) Tìm các vectơ hiệu:
\(\)\(\overrightarrow {NC} - \overrightarrow {MC} \); \(\overrightarrow {AC} - \overrightarrow {BC} \); \(\overrightarrow {AB} - \overrightarrow {ME} \).
c) Chứng minh \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \)
Phương pháp giải - Xem chi tiết
a) Chỉ ra các hình bình hành, từ đó suy ra các vectơ bằng nhau và vận dụng quy tắc hình bình hành.
b) Quy tắc hiệu: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \), quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \) và thay thế các vectơ bằng nhau \(\overrightarrow {ME} = \overrightarrow {AD} \)
c) Thay thế các vectơ bằng nhau \(\overrightarrow {AN} = \overrightarrow {MC} \); sử dụng quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (với ABCD là hình bình hành)
Lời giải chi tiết
a) Ta có: \(\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)
Suy ra \(\overrightarrow {MC} = \overrightarrow {CE} \)
+) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE} \)
+) ABCD là hình bình hành nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
\(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM} \)
+) Ta có \(\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC} = \overrightarrow {AM} \)
\(\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE} \) (vì AMED là hình bình hành)
b) Ta có:
+) \(\overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM} \)
+) \(\overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
+) \(\overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
c) Ta có:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} \)
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Từ đó suy ra \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \) (đpcm)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo timdapan.com"







