Bài 87 trang 53 SBT toán 7 tập 2
Giải bài 87 trang 53 sách bài tập toán 7. Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy. a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B...
Đề bài
Cho góc \(xOy\) khác góc bẹt, điểm \(A\) thuộc cạnh \(Ox,\) điểm \(B\) thuộc cạnh \(Oy.\)
a) Hãy tìm điểm \(M\) nằm trong góc \(xOy,\) cách đều \(Ox, Oy\) và cách đều \(A, B.\)
b) Nếu \(OA = OB\) thì có bao nhiêu điểm \(M\) thỏa mãn các điều kiện trong câu a?
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Điểm cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó
+) Điểm nằm trên đường trung trực của đoạn thẳng cách đều hai đầu mút của đoạn thẳng đó
+) Trong tam giác cân, đường phân giác của góc tại đỉnh cũng là đường trung trực của tam giác cân đó.
Lời giải chi tiết
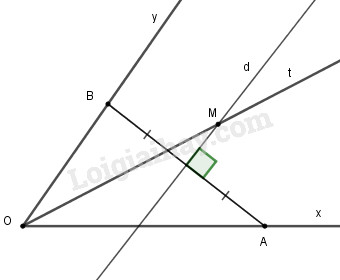
a)
- Điểm nằm trong góc \(xOy\) và cách đều hai cạnh \(Ox\) và \(Oy\) nên nó thuộc tia phân giác \(Ot\) của \(\widehat {xOy}\).
- Điểm cách đều 2 điểm \(A\) và \(B\) thuộc đường thẳng \(d\) là đường trung trực của \(AB\)
Vậy \(M\) là giao điểm của đường trung trực của đoạn thẳng \(AB\) và tia phân giác \(Ot\) của \(\widehat {xOy}\)
b) Nếu \(OA = OB\)
\( \Rightarrow ∆OAB\) cân tại \(O\)
Từ đó, tia phân giác của \(\widehat {xOy}\) cũng là đường trung trực của \(AB.\) Vậy bất kỳ điểm \(M\) nào nằm trên tia phân giác của \(\widehat {xOy}\) đều thỏa mãn điều kiện câu a.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 87 trang 53 SBT toán 7 tập 2 timdapan.com"







