Bài 85 trang 53 SBT toán 7 tập 2
Giải bài 85 trang 53 sách bài tập toán 7. Cho bốn điểm A, B, C, D như hình dưới. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
Đề bài
Cho bốn điểm \(A, B, C, D\) như trên hình 18. Hãy tìm một điểm \(M\) sao cho tổng \(MA + MB + MC + MD\) là nhỏ nhất.
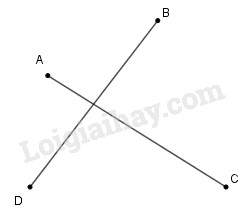
Hình 18
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong một tam giác:
+) Hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
+) Độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại
Lời giải chi tiết
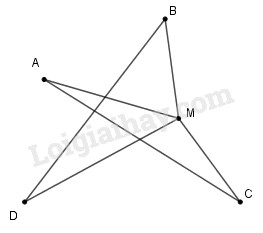
Với \(M\) là điểm bất kỳ.
Ta có \(M\) không trùng với giao điểm của \(AC\) và \(BD\)
Trong \(∆MBD\) ta có:
\(MB + MD > BD\) (bất đẳng thức tam giác)
Trong \(∆MAC\) ta có:
\(MA + MC > AC\) (bất đẳng thức tam giác)
Nếu \(M\) trùng với giao điểm \(AC\) và \(BD\)
\( \Rightarrow MA + MC = AC\)
\(MB + MD = BD\)
Vậy \(MA + MC ≥ AC\)
\(MB + MD ≥ BD\)
(dấu bằng xảy ra khi \(M\) trùng với giao điểm của \(AC\) và \(BD)\)
\( \Rightarrow MA + MB + MC + MD \)\(≥ AC + BD\)
Vậy \(MA + MB + MC + MD \)\(= AC + BD\) bé nhất khi đó \(M\) là giao điểm của \(AC\) và \(BD\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 85 trang 53 SBT toán 7 tập 2 timdapan.com"







