Bài 86 trang 53 SBT toán 7 tập 2
Giải bài 86 trang 53 sách bài tập toán 7.Cho hình 19 trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng:...
Đề bài
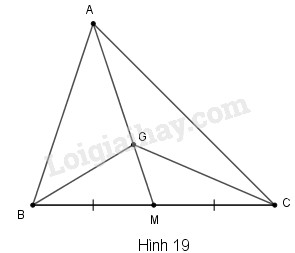
Cho hình 19 trong đó \(G\) là trọng tâm của tam giác \(ABC.\) Chứng minh rằng:
a) \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\)
b) \({S_{GMB}} = {S_{GMC}}\)
c) \({S_{AGB}} = {S_{AGC}} = {S_{BGC}}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Ba đường trung tuyến của tam giác giao nhau tại 1 điểm. Điểm đó cách đỉnh một đoạn bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến tương ứng.
+) Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
+) Hai tam giác có chung chiều cao thì tỉ số diện tích bằng với tỉ số cạnh đáy.
Lời giải chi tiết
a) \(G\) là trọng tâm của \(∆ABC\)
\( \Rightarrow GA = 2GM\) (tính chất đường trung tuyến)
Ta có \(∆AGC\) và \(∆GMC\) có chung đường cao kẻ từ đỉnh \(C\) đến \(AM.\)
Cạnh đáy \(GA = 2GM\)
Suy ra: \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\) (1)
b) Ta có: \(∆GMB\) và \(∆GMC\) có cạnh đáy \(MB = MC,\) chung chiều cao kẻ từ đỉnh \(G\) đến cạnh \(BC\)
\({S_{GMB}} = {S_{GMC}}\) (2)
c) Hai tam giác \(AGB\) và \(GMB\) có chung chiều cao kẻ từ đỉnh \(B\) đến cạnh \(AM.\)
Mà \(AG = 2GM\) (chứng minh trên)
Suy ra:
\(\eqalign{
& {S_{AGB}} = 2{{\rm{S}}_{GMB}}\left( 3 \right) \cr
& {S_{BGC}} = {S_{GMB}} + {S_{GMC}} = 2{S_{GMB}}\left( 4 \right) \cr} \)
Từ (1), (2), (3) và (4) suy ra: \({{\rm{S}}_{AGC}} = {S_{AGB}} = {S_{BGC}}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 86 trang 53 SBT toán 7 tập 2 timdapan.com"







