Giải bài 8 trang 75 SBT toán 10 - Cánh diều
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
Đề bài
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng định lí cosin cho hai tam giác ∆ABC và ∆ADB để tính độ dài AC và BD
Bước 2: Xét mối liên hệ của các góc trong hình bình hành
Bước 3: Biến đổi các đẳng thức. Kết luận
Lời giải chi tiết
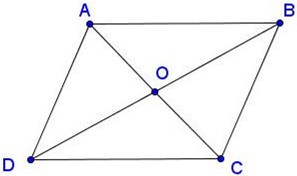
- Áp dụng định lí cosin cho ∆ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\)\( \Leftrightarrow {m^2} = {a^2} + {b^2} - 2ab.\cos \widehat {ABC}\) (1)
- Áp dụng định lí cosin cho ∆ADB ta có:
\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {DAB}\)\( \Leftrightarrow {n^2} = {a^2} + {b^2} - 2ab.\cos \widehat {DAB}\) (2)
Do ABCD là hình bình hành nên AD // BC \( \Rightarrow \widehat {ABC} + \widehat {DAB} = {180^0}\) \( \Rightarrow \cos \widehat {ABC} = - \cos \widehat {DAB}\) (3)
Từ (1), (2), (3) ta có: \({m^2} + {n^2} = 2({a^2} + {b^2}) - 2ab(\cos \widehat {ABC} + \cos \widehat {DAB})\)\( \Leftrightarrow {m^2} + {n^2} = 2({a^2} + {b^2})\) (ĐPCM)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 75 SBT toán 10 - Cánh diều timdapan.com"







