Bài 8 trang 184 SBT toán 8 tập 2

Đề bài

Tam giác \(ABC\) vuông ở \(C\) có \(AC = 6cm, AB = 9cm,\) \(CD\) là đường cao \((D ∈ AB).\) Độ dài \(BD\) bằng:

A. \(8cm;\)                                    B. \(6cm;\)

C. \(5cm;\)                                    D. \(4cm.\)

Hãy chọn câu trả lời đúng.

Lời giải chi tiết

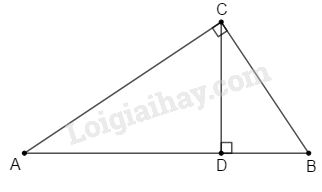
Áp dụng định lí Pytago vào tam giác vuông \(ABC\), ta có:

\(\begin{array}{l}
A{B^2} = A{C^2} + B{C^2}\\
\Rightarrow B{C^2} = A{B^2} - A{C^2}\\
\Rightarrow B{C^2} = {9^2} - {6^2} = 45
\end{array}\)

Xét \(ΔBDC\) và \(ΔBCA\) có:

\(\widehat B\) chung

\(\widehat {BDC} = \widehat {BCA} = {90^o}\)

\( \Rightarrow ΔBDC \backsim ΔBCA\) (g.g)

\(\begin{array}{l}
\Rightarrow \dfrac{{BD}}{{BC}} = \dfrac{{BC}}{{BA}}\\
\Rightarrow BD = \dfrac{{B{C^2}}}{{BA}} = \dfrac{{45}}{9} = 5\,\left( {cm} \right)
\end{array}\)

Chọn C.