Bài 5 trang 184 SBT toán 8 tập 2
Giải bài 5 trang 184 sách bài tập toán 8. Tứ giác ABCD có AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm, đường chéo BD = 6cm. Chứng minh rằng ABCD là hình thang.
Đề bài
Tứ giác \(ABCD\) có \(AB = 3cm, BC = 10cm,\) \(CD = 12cm, AD = 5cm,\) đường chéo \(BD = 6cm.\) Chứng minh rằng \(ABCD\) là hình thang.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tam giác này có ba cạnh tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Dấu hiệu nhận biết hai đường thẳng song song: Nếu \(c\) cắt hai đường thẳng \(a\) và \(b\) trong các góc tạo thành có cặp góc so le trong bằng nhau thì \(a//b\).
- Tứ giác có hai cạnh đối song song là hình thang.
Lời giải chi tiết
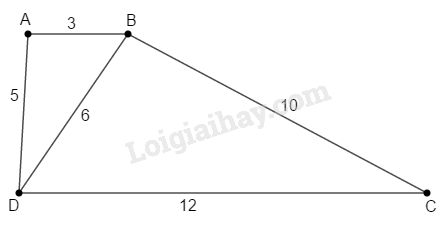
Ta có:
\(\begin{array}{l}
\dfrac{{AB}}{{BD}} = \dfrac{3}{6} = \dfrac{1}{2}\\
\dfrac{{AD}}{{BC}} = \dfrac{5}{{10}} = \dfrac{1}{2}\\
\dfrac{{BD}}{{DC}} = \dfrac{6}{{12}} = \dfrac{1}{2}\\
\Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}} = \dfrac{1}{2}
\end{array}\)
Xét \(ΔABD \) và \( ΔBDC\) có:
\(\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}= \dfrac{1}{2}\) (cmt)
\( ⇒ ΔABD \backsim ΔBDC\) (c.c.c)
\( ⇒ \widehat {ABD} = \widehat {BDC}\)
Mà \( \widehat {ABD} \) và \(\widehat {BDC}\) ở vị trí so le trong nên \(AB // CD\).
Tứ giác \(ABCD\) có \(AB//CD\) (cmt) nên là hình thang.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 184 SBT toán 8 tập 2 timdapan.com"







