Bài 8 trang 164 SBT toán 9 tập 2

Đề bài

Diện tích xung quanh của một hình trụ là \(10m^2\) và diện tích toàn phần của nó là \(14m^2\). Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy \(\pi  \approx 3,14,\) làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải chi tiết

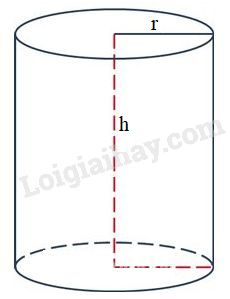
Diện tích toàn phần của hình trụ là: \({S_{tp}} = S_{xq} + 2S_đ\)

Diện tích của một đáy là:

\(\displaystyle S_đ={{{S_{TP}} - {S_{xq}}} \over 2} = {{14 - 10} \over 2}\)\(\, = 2\;({m^2})\)

Diện tích đáy là: \(S_{đ}= \pi r^2\) 

\(\displaystyle \Rightarrow {r^2} = {S_đ \over \pi } \approx {2 \over {3,14}} \approx 0,64\;({m^2})\)

Suy ra bán kính đáy \(  r = 0,8\;(m)\)

Diện tích xung quanh hình trụ là: \({S_{xq}} = 2πrh\).

\(\displaystyle  \Rightarrow h = {{{S_{xq}}} \over {2\pi r}} = {{10} \over {2.3,14.0,8}} \)\(\,\approx 1,99\;(m)\).