Giải bài 7.56 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Một bể chứa nước hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) được đặt trên một mái nhà nghiêng
Đề bài
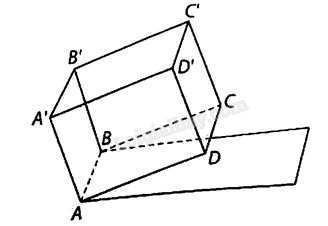
Một bể chứa nước hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc \({10^ \circ },AB = 1{\rm{\;m}},AD = 1,5{\rm{\;m}}\), \(AA' = 1{\rm{\;m}}\). Đáy bể là hình chữ nhật \(ABCD\). Các điểm \(A,B\) cùng ở độ cao \(5{\rm{\;m}}\) (so với mặt đất), các điểm \(C,D\) ở độ cao lớn hơn so với độ cao của các điểm \(A,B\). Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng \(\left( {ABB'A'} \right)\) và mặt đáy của bể là \(80{\rm{\;cm}}\). Tính thế tích của phần nước trong bể.
Phương pháp giải - Xem chi tiết
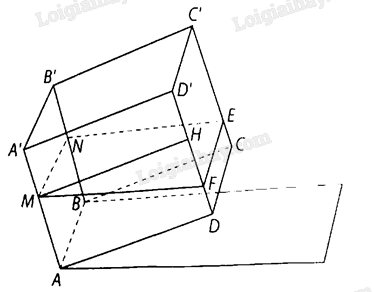
Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB'A'} \right),EF\) là đường mép nước trên mặt \(\left( {CDD'C'} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD'\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Tính: \({S_1} = {S_{DCEF}};{S_2} = {S_{ABNM}}\).
Tính \(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD\)
Lời giải chi tiết

Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB'A'} \right),EF\) là đường mép nước trên mặt \(\left( {CDD'C'} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD'\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Ta có: \({S_1} = {S_{DCEF}} = DF \cdot CD \approx 0,62\left( {{\rm{\;}}{{\rm{m}}^2}} \right);{S_2} = {S_{ABNM}} = AB \cdot AM = 0,8\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\).
Vậy thể tích phần nước trong bể là
\(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD = \frac{1}{3} \cdot \left( {0,62 + 0,8 + \sqrt {0,62 \cdot 0,8} } \right) \approx 0,71\left( {{\rm{\;}}{{\rm{m}}^3}} \right).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 7.56 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống timdapan.com"







