Giải bài 7.4 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a.
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a. Gọi \(M\), N lần lượt là trung điểm các cạnh \(SA,AB\)
a) Tính góc giữa các cặp đường thẳng sau: \(MN\) và \(SD;MO\) và \(SB\)
b) Tính tang của góc giữa hai đường thẳng \(SN\) và \(BC\).
Phương pháp giải - Xem chi tiết
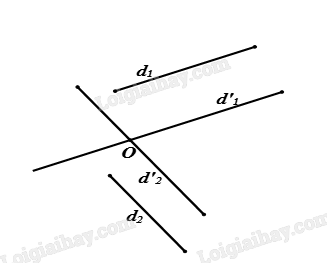
Từ \(O\) dựng các đường thẳng \(d'_1,d'_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d'_1,d'_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý :
Áp dụng định lý Pytago đảo để chứng minh tam giác vuông
Áp dụng tính chất đường trung bình tam giác
Áp dụng tính chất \(\left\{ \begin{array}{l}a//b\\a \bot c\end{array} \right. \Rightarrow b \bot c\)
Lời giải chi tiết
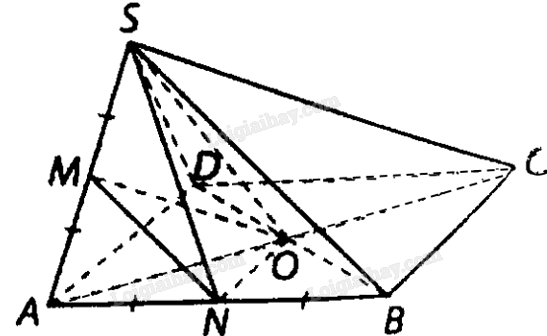
a) Ta có: \(B{D^2} = S{B^2} + S{D^2} = 2{a^2}\) nên \(\Delta SBD\) vuông tại \(S\), mà \(MN//SB\), suy ra \(\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }\).
Với O là giao điểm của \(AC\) và \(BD\) thì \(MO//SC\).
Khi đó \(\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }\).
b) Vì \(ON{\rm{ }}//BC\) nên \(\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}\).
Ta có \(SO = \frac{{a\sqrt 2 }}{2};ON = \frac{a}{2}\) và tam giác \(SNO\)vuông tại O nên \({\rm{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 \).
Vậy \({\rm{tan}}\left( {SN,BC} \right) = \sqrt 2 \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 7.4 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống timdapan.com"







