Bài 7 trang 102 SBT toán 7 tập 2

Đề bài

a) Chứng minh rằng: Nếu tam giác \(ABC\) có đường trung tuyến \(AM\) bằng nửa cạnh \(BC\) thì tam giác đó vuông tại \(A.\)

b) Ứng dụng: Một tờ giấy bị rách ở mép (h.110). Hãy dùng thước và compa vẽ đường vuông góc với \(AB\) tại \(A.\)

Hướng dẫn: Vẽ điểm \(C\) sao cho \(CA = CB,\) rồi vẽ điểm \(E\) thuộc tia đối của tia \(CB\) sao cho \(CE = CB.\) 

Lời giải chi tiết

a)

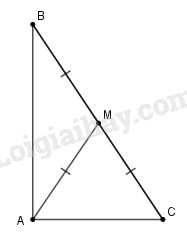
Xét tam giác \(AMB\) cân tại \(M\) (vì \(MA = MB = \dfrac{{BC}}{2}\) ) nên \(\widehat {MBA} = \widehat {MAB}\) (tính chất) 

Xét tam giác \(AMC\) cân tại \(M\) (vì \(MA = MC = \dfrac{{BC}}{2}\) ) nên \(\widehat {MCA} = \widehat {MAC}\) (tính chất)

Suy ra \(\widehat {MBA} + \widehat {MCA} = \widehat {MAB} + \widehat {MAC}\)\( = \widehat {BAC}\)  hay \(\widehat {ABC} + \widehat {ACB} = \widehat {BAC}\) (1)

Xét tam giác \(ABC\) có \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} \)\(= 180^\circ \) (2) (định lý tổng ba góc trong tam giác)

Từ (1) và (2) suy ra \(\widehat {BAC} = \dfrac{{\widehat {ABC} + \widehat {BAC} + \widehat {ACB}}}{2} \)\(= \dfrac{{180^\circ }}{2} = 90^\circ \)

Hay tam giác \(ABC\) vuông tại \(A.\)

b) 

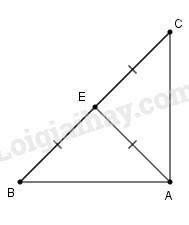
Cách vẽ:

+) Vẽ điểm \(E\) sao cho \(EA = EB\)

+) Vẽ đường tròn tâm \(E\) bán kính \(EB\), sau đó kẻ đường kính \(BC.\)

+) Nối \(AC\) ta có \(AC \bot AB\) tại \(A.\)

Chứng minh:

Theo cách vẽ ta có \(EB = EA = EC = \dfrac{{BC}}{2}\) hay tam giác \(ABC\) có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền nên theo câu a) ta có \(\Delta ABC\) vuông tại \(A\) hay \(AC \bot AB\) tại \(A.\)