Bài 6 trang 102 SBT toán 7 tập 2
Giải bài 6 trang 102 sách bài tập toán 7. Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: a) BD là đường thẳng trung trực của AE;...
Đề bài
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD.\) Kẻ \(DE ⊥ BC (E ∈ BC).\) Gọi \(F\) là giao điểm của \(BA\) và \(ED.\) Chứng minh rằng:
a) \(BD\) là đường thẳng trung trực của \(AE;\)
b) \(DF = DC;\)
c) \(AD > DC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Các trường hợp bằng nhau của tam giác
+) Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó
+) Trong tam giác vuông, cạnh huyền có độ dài lớn nhất.
Lời giải chi tiết
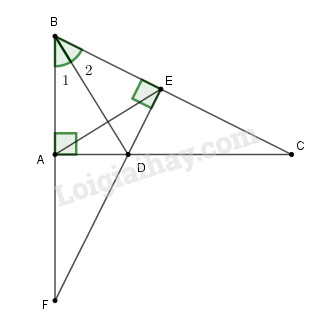
a) Xét tam giác vuông \(ABD\) và tam giác vuông \(EBD\) có:
+) \(\widehat {{B_1}} = \widehat {{B_2}}\) (do \(BD\) là phân giác góc \(B\))
+) \(BD\) cạnh chung
Suy ra \(\Delta ABD = \Delta EBD\left( {ch - gn} \right)\) nên \(BA = BE;DA = DE\) (các cạnh tương ứng)
Do đó \(B,D\) cùng thuộc đường trung trực của \(AE\) hay \(BD\) là đường trung trực của \(AE.\)
b) Xét tam giác vuông \(AFD\) và tam giác vuông \(ECD\) có:
+) \(\widehat {ADF} = \widehat {EDC}\) (hai góc đối đỉnh)
+) \(AD = DE\) (theo câu a)
Suy ra \(\Delta AFD = \Delta ECD\left( {g - c - g} \right)\) nên \(DF = DC\) (hai cạnh tương ứng)
c) Xét tam giác vuông \(ADF\) có \(DF\) là cạnh huyền nên \(DF > AD\)
Mà \(DF = DC\) (theo câu b), suy ra \(DC > AD.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 102 SBT toán 7 tập 2 timdapan.com"







