Bài 1 trang 101 SBT toán 7 tập 2
Giải bài 1 trang 101 sách bài tập toán 7. Cho hình 107, trong đó góc B=40 độ, góc D=130 độ, AB//DE. Tính góc BCD.
Đề bài
Cho hình 107 trong đó \(\widehat B = 40^\circ ,\,\widehat D = 130^\circ ,AB//DE.\) Tính \(\widehat {BCD}\).
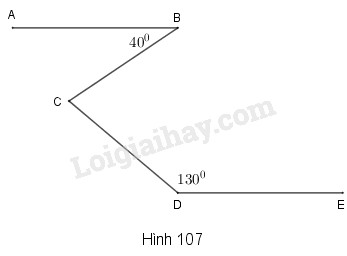
Phương pháp giải - Xem chi tiết
Kẻ thêm \(Cx//AB\)
Sử dụng:
+) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các gặp góc so le trong bẳng nhau và cặp góc trong cùng phía bù nhau.
+) Hai góc bù nhau có tổng bằng \(180^\circ .\)
Lời giải chi tiết
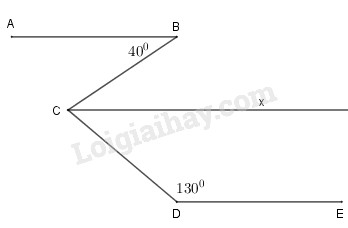
Kẻ thêm \(Cx//AB\) mà \(AB//DE \Rightarrow Cx//DE\)
+) Vì \(AB//Cx\) nên \(\widehat {BCx} = \widehat {ABC} = 40^\circ \) (cặp góc so le trong bằng nhau)
+) Vì \(Cx//CD\) nên \(\widehat {DCx} + \widehat {CDE} = 180^\circ \) (hai góc trong cũng phía bù nhau)
\( \Leftrightarrow \widehat {DCx} = 180^\circ - \widehat {CDE} \)\(= 180^\circ - 130^\circ = 50^\circ \)
Từ đó ta có: \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} \)\(= 40^\circ + 50^\circ = 90^\circ \)
Vậy \(\widehat {BCD} = 90^\circ .\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 101 SBT toán 7 tập 2 timdapan.com"







