Bài 4 trang 102 SBT toán 7 tập 2
Giải bài 4 trang 102 sách bài tập toán 7. So sánh các cạnh của tam giác CDE trên hình 109 biết rằng BE // CD.
Đề bài
So sánh các cạnh của tam giác \(CDE\) trên hình 109 biết rằng \(BE // CD.\)
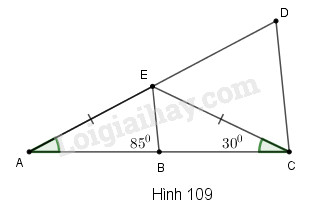
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các gặp góc đồng vị bẳng nhau.
+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau
+) Tổng ba góc trong tam giác bằng \(180^\circ \)
+) Hai góc kề bù có tổng số đo bằng \(180^\circ \)
+) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn
Lời giải chi tiết
Vì \(EB//CD\) nên \(\widehat {BCD} = \widehat {EBA} = 85^\circ \) (hai góc đồng vị bằng nhau)
Lại có \(\widehat {BCE} + \widehat {ECD} = \widehat {BCD}\) \( \Rightarrow \widehat {ECD} \)\(= \widehat {BCD} - \widehat {BCE} = 85^\circ - 30^\circ = 55^\circ \)
Tam giác \(ECA\) cân tại \(E\) có \(\widehat {EAC} = \widehat {ECA} = 30^\circ \)
Suy ra \(\widehat {AEC} = 180^\circ - \left( {\widehat {EAC} + \widehat {ECA}} \right) \)\(= 120^\circ \)
Ta có: \(\widehat {AEC} + \widehat {CED} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CED} = 180^\circ - \widehat {AEC} = 60^\circ \)
Xét tam giác \(ECD\) có \(\widehat {DEC} + \widehat {ECD} + \widehat {EDC} \)\(= 180^\circ \)
\( \Rightarrow \widehat {EDC} = 180^\circ - \left( {\widehat {DEC} + \widehat {ECD}} \right)\) \( = 180^\circ - \left( {55^\circ + 60^\circ } \right) = 65^\circ \)
Suy ra \(\widehat {ECD} < \widehat {CED} < \widehat {EDC}\,\)\(\,\left( {55^\circ < 60^\circ < 65^\circ } \right)\)
Do đó: \(ED < DC < EC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4 trang 102 SBT toán 7 tập 2 timdapan.com"







