Giải bài 6 trang 76 SGK Toán 7 tập 2 - Chân trời sáng tạo
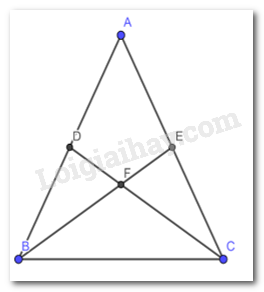
Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.
Đề bài
Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.
Phương pháp giải - Xem chi tiết
- Ta chứng minh F là trọng tâm tam giác ABC
- Sau đó chứng minh CD = BE
- Áp dụng định lí về trọng tâm tam giác ta tính các đoạn DF, EF
Lời giải chi tiết
Vì BE, CD là 2 trung tuyến của tam giác ABC
NÊn E, D lần lượt là trung tuyến của AB và AC
\( \Rightarrow AD = AE = \dfrac{1}{2}AB = \dfrac{1}{2}AC\)
Xét tam giác ADC và tam giác AEB có :
AD = AE
Góc A chung
AB = AC (tam giác ABC cân tại A theo giả thiết)
\( \Rightarrow \Delta ADC = \Delta AEB(c - g - c)\)
\( \Rightarrow BE = CD\)(cạnh tương ứng)
Vì F là giao 2 trung tuyến nên F là trọng tâm tam giác ABC
\( \Rightarrow CF = BF = \dfrac{2}{3}BE = \dfrac{2}{3}CD\) ( định lí về trung tuyến đi qua trọng tâm tam giác )
\( \Rightarrow \dfrac{1}{3}BE = \dfrac{1}{3}CD \Rightarrow DF = FE = \dfrac{1}{3}.9cm = 3cm\)
\( \Rightarrow \) DF = 3 cm
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 6 trang 76 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







