Giải bài 4 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến. a) Chứng minh rằng BM = CN b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Đề bài
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Phương pháp giải - Xem chi tiết
- Ta chứng minh 2 tam giác bằng nhau để từ đó chứng minh 2 đoạn thẳng bằng nhau
- Ta chứng minh I là trọng tâm tam giác ABC và chứng minh AH là trung tuyến của tam giác ABC và H là trung điểm của BC
Lời giải chi tiết
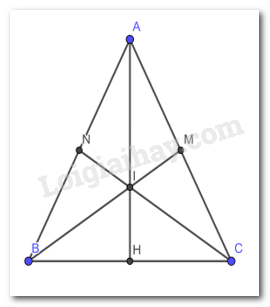
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







