Giải bài 56 trang 63 SBT toán 10 - Cánh diều
Hai địa điểm A và B cách hai bởi một con sông (coi hai bờ sông song song).
Đề bài
Hai địa điểm A và B cách hai bởi một con sông (coi hai bờ sông song song). Người ta muốn xây một chiếc cầu bắc vuông góc với bờ sông để có thể đi từ A đến B. Với các số liệu (tính theo đơn vị km) cho trên Hình 28, tìm \(x\) (km) để xác định vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.
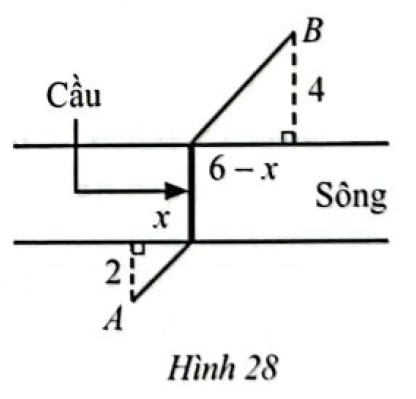
Phương pháp giải - Xem chi tiết
+ Gọi chân cầu phía A là M, chân cầu phía B là N. Tính AM, BN dựa vào Pytago.
+ Giải phương trình \(BM = 2AM\) có dạng \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \)
\(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
Lời giải chi tiết
Gọi chân cầu phía A là M, chân cầu phía B là N.
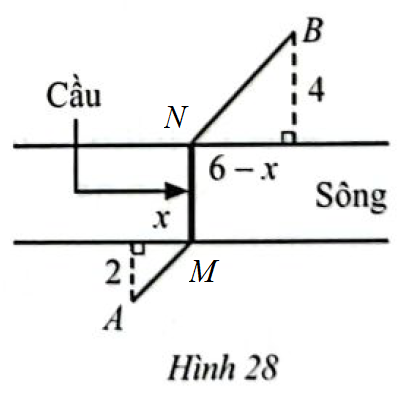
Dựa vào hình 28, áp dụng định lý Pytago, ta có:
\(AM = \sqrt {{x^2} + {2^2}} = \sqrt {{x^2} + 4} ,BN = \sqrt {{{\left( {6 - x} \right)}^2} + {4^2}} = \sqrt {{x^2} - 12x + 52} \)
Theo đề bài, ta có: \(BM = 2AM \Leftrightarrow \sqrt {{x^2} - 12x + 52} = 2\sqrt {{x^2} + 4} \)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 4 \ge 0\\{x^2} - 12x + 52 = 4\left( {{x^2} + 4} \right)\end{array} \right.\\ \Leftrightarrow {x^2} - 12x + 52 = 4{x^2} + 16\\ \Leftrightarrow 3{x^2} + 12x - 36 = 0\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x = - 6\end{array} \right.\end{array}\)
Do \(x > 0\) nên \(x = 2\).
Vậy với \(x = 2\) km thì khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 56 trang 63 SBT toán 10 - Cánh diều timdapan.com"







