Giải bài 52 trang 100 SBT toán 10 - Cánh diều
Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau:
Đề bài
Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau:
a) \(\overrightarrow {AM} = \overrightarrow {CB} \)
b) \(\overrightarrow {AN} = - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
c) \(\overrightarrow {PA} - \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \)
Phương pháp giải - Xem chi tiết
Bước 1: Xác định hướng và độ lớn các vectơ (sử dụng các quy tắc cộng, trừ, quy tắc hình bình hành,…)
Bước 2: Xác định vị trí các điểm M, N, P dựa vào hướng và độ lớn các vectơ tương ứng rồi kết luận
Lời giải chi tiết
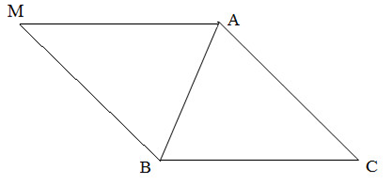
a) Theo giả thiết, \(\overrightarrow {AM} = \overrightarrow {CB} \)\( \Rightarrow \) \(\overrightarrow {AM} \) cùng hướng và có độ lớn bằng \(\overrightarrow {CB} \)
Vậy điểm M thuộc đường thẳng đi qua A, song song với BC sao cho AMBC là hình bình hành
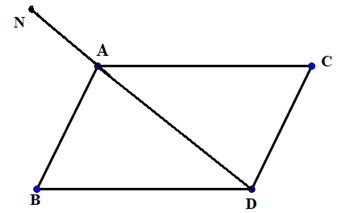
b) Theo giả thiết, \(\overrightarrow {AN} = - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
Dựng hình bình hành ABDC, theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)\( \Rightarrow \overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AD} \)
Vậy điểm N thuộc tia đối của tia AD thỏa mãn \(AN = \frac{1}{2}AD\)
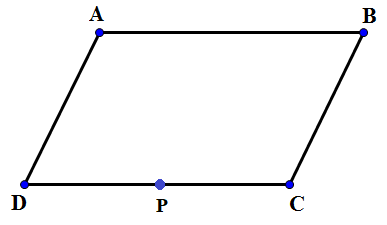
c) Theo giả thiết, \(\overrightarrow {PA} - \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {PC} = - \frac{1}{2}\overrightarrow {BA} \)
Dựng hình bình hành ABCD. Khi đó P là trung điểm của CD
Vậy điểm P là trung điểm đoạn thẳng CD thỏa mãn ABCD là hình bình hành
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 52 trang 100 SBT toán 10 - Cánh diều timdapan.com"







