Bài 5.11 trang 15 SBT Vật lí 9

Đề bài

Cho mạch điện có sơ đồ như hình 5.6, trong đó điện trở \(R_1=6Ω\); dòng điện mạch chính có cường độ \(I=1,2A \) và dòng điện đi qua điện trở \(R_2\) có cường độ \(I_2=0,4A\).

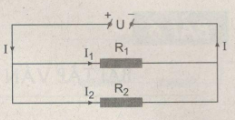
b. Tính hiệu điện thế \(U\) đặt vào hai đầu đoạn mạch.

c. Mắc một điện trở \(R_3\) vào mạch điện trên , song song với \(R_1\) và \(R_2\) thì dòng điện trong mạch chính có cường độ là \(1,5A\). Tính \(R_3\) và điện trở tương đương \(R_{tđ}\) của đoạn mạch này khi đó.

Lời giải chi tiết

a) Mạch gồm \(R_1//R_2\), nên ta có:

+ Hiệu điện thế qua \(R_1\) bằng hiệu điện thế qua \(R_2\) và bằng hiệu điện thế của toàn mạch: \(U=U_1=U_2\)

+ Cường độ dòng điện trong mạch: \(I=I_1+I_2\)

Ta suy ra, cường độ dòng điện qua điện trở \(R_1\) là:

\({I_1} = I - {I_2} = 1,2 - 0,4 = 0,8{\rm{A}}\)

Lại có:

\(I_1=\dfrac{U_1}{R_1}=\dfrac{U}{R_1}=0,8A\) (1)

\(I_2=\dfrac{U_2}{R_2}=\dfrac{U}{R_2}=0,4A\) (2)

Lấy \(\dfrac{(1)}{(2)}\) ta được: 

\(\begin{array}{l}\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{\dfrac{U}{{{R_1}}}}}{{\dfrac{U}{{{R_2}}}}} = \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{0,8}}{{0,4}} = 2\\ \Rightarrow {R_2} = 2{R_1} = 2.6 = 12\Omega \end{array}\)

b) Ta có: \(U=U_1=U_2\)

Hiệu diện thế qua điện trở \(R_1\) là: \({U_1} = {I_1}.{R_1} = 0,8.6 = 4,8V \)

\(\Rightarrow U = {U_1} = {U_2} = 4,8V\)

Vậy hiệu điện thế đặt vào hai đầu đoạn mạch là: \(U=4,8V\)

c)

Điện trở tương đương của mạch là:

\(R_{tđ} = \dfrac{U}{I} =\dfrac{4,8}{1,5}=3,2\Omega\)

Điện trở tương đương của điện trở \(R_1\) và \(R_2\) là \(R_{12}\)

\({R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)\(=\dfrac{6.12}{6+12}=4\Omega\)

Lại có: \(R_{12}//R_3\)

Ta có:

\(\eqalign{
& {1 \over {{R_{tđ}}}} = {1 \over {{R_3}}} + {1 \over {{R_{12}}}} \cr 
& \Rightarrow {1 \over {{R_3}}} = {1 \over {{R_{tđ}}}} - {1 \over {{R_{12}}}} \cr 
& \Rightarrow {1 \over {{R_3}}} = {1 \over {3,2}} - {1 \over 4} = {1 \over {16}} \cr 
& \Rightarrow {R_3} = 16\Omega \cr} \)

Vậy điện trở \(R_3=16\Omega\) và điện trở tương đương của đoạn mạch là \(R_{tđ}=3,2 \Omega\)