Giải bài 5 trang 57 SGK Toán 8 tập 2– Chân trời sáng tạo
Cho tam giác
Đề bài
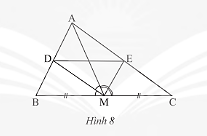
Cho tam giác \(ABC\) có đường trung tuyến \(AM\). Đường phân giác của góc \(AMB\) cắt \(AB\) tại \(D\) và đường phần giác góc \(AMC\) cắt \(AC\) tại \(E\) (Hình 8). Chứng minh \(DE//BC\).
Phương pháp giải - Xem chi tiết
- Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
- Định lí Thales đảo:
Nếu một đường thẳng cắt hai cạnh của tam giác và vạch ra trên đó các đoạn thẳng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
Vì \(MD\) là tia phân giác của góc \(\widehat {AMB}\) nên \(\frac{{AD}}{{DB}} = \frac{{AM}}{{BM}}\) (1)
Vì \(ME\) là tia phân giác của góc \(\widehat {AMC}\) nên \(\frac{{AE}}{{EC}} = \frac{{AM}}{{MC}}\)(2);
Mà \(M\) là trung điểm của \(BC\) nên \(BM = MC\) (3)
Từ (1); (2); (3) \( \Rightarrow \frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)
Xét tam giác \(ABC\) có: \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}\)
Do đó, \(DE//BC\)(Định lí Thales đảo).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 trang 57 SGK Toán 8 tập 2– Chân trời sáng tạo timdapan.com"







