Bài 4.43 trang 113 SBT đại số 10

Đề bài

Cho hàm số \(f(x) = \dfrac{{{x^2} - 4}}{{(x - 2)(2x + 3)}}\). Tìm các khoảng mà trong đó \(f(x)\) nhận giá trị dương

A. \(( - \infty ; - 2)\) và \(( - \dfrac{3}{2}; + \infty )\)

B. \(( - \infty ; - 2)\), \(( - \dfrac{3}{2};2)\) và \((2, + \infty )\)

C. \(( - 2; - \dfrac{3}{2})\)

D. \(( - 2; - \dfrac{3}{2})\) và \(( - \dfrac{3}{2};2)\)

Lời giải chi tiết

\(f(x)\) không xác định khi \(x = 2\), mà\(2 \in ( - \dfrac{3}{2}; + \infty )\), vậy A sai

Xét \(x =  - \dfrac{7}{4}\) thì \({x^2} - 4 < 0;x - 2 < 0;2x + 3 < 0\)

\( \Rightarrow f(x) < 0\). Loại đáp án C và D.

Vậy chọn B.

Tự luận:

Lập bảng xét dấu:

ĐK: \(\left\{ \begin{array}{l}x - 2 \ne 0\\x + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne  - 2\end{array} \right.\)

Ta có: \(f\left( x \right) = \dfrac{{{x^2} - 4}}{{\left( {x - 2} \right)\left( {2x + 3} \right)}}\) \( = \dfrac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {2x + 3} \right)}} = \dfrac{{x + 2}}{{2x + 3}}\)

\(f\left( x \right) = 0 \Leftrightarrow x + 2 = 0\) \( \Leftrightarrow x =  - 2\)

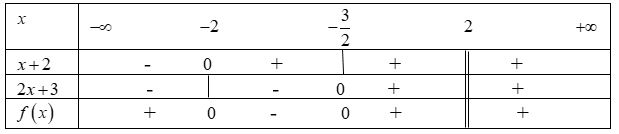
Bảng xét dấu:

Từ bảng xét dấu ta suy ra \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 2\\ - \dfrac{3}{2} < x < 2\\x > 2\end{array} \right.\)