Bài 44 trang 143 SBT toán 7 tập 1

Đề bài

Cho tam giác \(AOB\) có \(OA = OB.\) Tia phân giác của góc \(O\) cắt \(AB\) ở \(D.\) Chứng minh rằng:

a) \(DA = DB\)

b) \(O{\rm{D}} \bot\, AB\)

Lời giải chi tiết

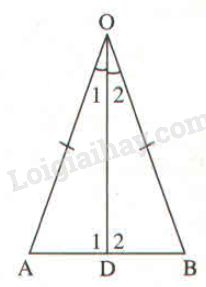
a) Xét \(∆AOD\) và \(∆BOD\), ta có:

\(OA = OB\) (gt)

\(\widehat {AO{\rm{D}}} = \widehat {BO{\rm{D}}}\) (vì \(OD\) là tia phân giác góc \(O\))

\(OD\) cạnh chung

\( \Rightarrow   ∆AOD = ∆BOD\) (c.g.c)

\( \Rightarrow  DA = DB\) (hai cạnh tương ứng)

b) \(∆AOD = ∆BOD\) (chứng minh trên)

\( \Rightarrow \widehat {{D_1}} = \widehat {{D_2}}\) (hai góc tương ứng)

Ta có: \(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ\) (hai góc kề bù)

\(\Rightarrow \widehat {{D_1}} = \widehat {{D_2}} = 90^\circ \)

Vậy \(O{\rm{D}} \bot \,AB\).