Bài 42 trang 111 SBT toán 9 tập 1

Cho hình:

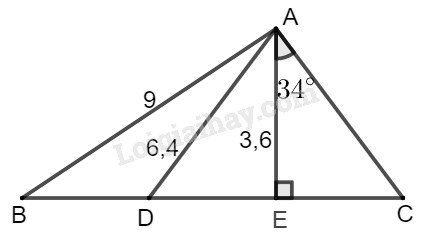
Biết: 

\(AB = 9cm,AC = 6,4cm\)

\(AN = 3,6cm,\widehat {AN{\rm{D}}} = 90^\circ ,\widehat {DAN} = 34^\circ \)

Hãy tính:

LG a

\(CN;\)

Phương pháp giải:

+) Sử dụng: Định lý Pytago vào tam giác \(ABC\) vuông tại \(A\).

\(A{B^2} + A{C^2} = B{C^2}\)

+) Sử dụng các tỉ số lượng giác của góc nhọn như sau: 

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Lời giải chi tiết:

Áp dụng định lí Pytago vào tam giác vuông \(ANC\), ta có: 

 \(A{C^2} = A{N^2} + N{C^2}\) 
\(\Rightarrow N{C^2} = A{C^2} - A{N^2}\)
\(\Rightarrow NC = \sqrt {A{C^2} - A{N^2}}\)\( = \sqrt {6,{4^2} - 3,{6^2}} = \sqrt {28}\)
\(\Rightarrow NC = 5,2915\left( {cm} \right)\)

LG b

\(\widehat {ABN}\);

Phương pháp giải:

+) Sử dụng: Định lý Pytago vào tam giác \(ABC\) vuông tại \(A\).

\(A{B^2} + A{C^2} = B{C^2}\)

+) Sử dụng các tỉ số lượng giác của góc nhọn như sau: 

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Lời giải chi tiết:

Tam giác \(ANB\) vuông tại \(N\) nên ta có:

\(\sin \widehat {ABN} = \dfrac{{AN}}{{AB}} = \dfrac{{3,6}}{ 9} = 0,4\) 

\( \Rightarrow \widehat {ABN} \approx 23^\circ 35'\)

LG c

\(\widehat {CAN}\);

Phương pháp giải:

+) Sử dụng: Định lý Pytago vào tam giác \(ABC\) vuông tại \(A\).

\(A{B^2} + A{C^2} = B{C^2}\)

+) Sử dụng các tỉ số lượng giác của góc nhọn như sau: 

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Lời giải chi tiết:

Tam giác \(ANC\) vuông tại \(N\) nên ta có:

\(\eqalign{
& \cos \widehat {CAN} = {{AN} \over {AC}} \cr 
& = {{3,6} \over {6,4}} = {9 \over {16}} = 0,5625 \cr 
& \Rightarrow \widehat {CAN} \approx 55^\circ 46' \cr} \) 

LG d

\(AD.\)

Phương pháp giải:

+) Sử dụng: Định lý Pytago vào tam giác \(ABC\) vuông tại \(A\).

\(A{B^2} + A{C^2} = B{C^2}\)

+) Sử dụng các tỉ số lượng giác của góc nhọn như sau: 

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Lời giải chi tiết:

Tam giác \(AND\) vuông tại \(N\) nên ta có:

\(\eqalign{
& \cos \widehat {NAD} = {{AN} \over {AD}} \cr 
& \Rightarrow AD = {{AN} \over {\cos \widehat {NAD}}} \cr 
& = {{3,6} \over {\cos 34^\circ }} \approx 4,3424 \cr} \)