Giải bài 41 trang 75 sách bài tập toán 8 – Cánh diều
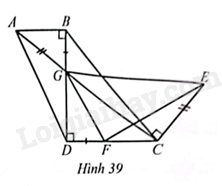
Hình thang \(ABCD\) ở Hình 39 có \(AB//CD,AB < CD,\widehat {ABD} = 90^\circ \). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(G\).
Đề bài
Hình thang \(ABCD\) ở Hình 39 có \(AB//CD,AB < CD,\widehat {ABD} = 90^\circ \). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(G\). Điểm \(E\) nằm trên đường vuông góc với \(AC\) tại \(C\) thỏa mãn \(CE = AG\) và đoạn thẳng \(GE\) không cắt đường thẳng \(CD\). Điểm \(F\) nằm trên đoạn thẳng \(DC\) và \(DF = GB\). Chứng minh:
a) \(\Delta FGD\backsim \Delta ECG\);
b) \(\Delta GDC\backsim \Delta GFE\);
c) \(\widehat {GFE} = 90^\circ \).
Phương pháp giải - Xem chi tiết
Áp dụng trường hợp đồng dạng thứ hai của tam giác: cạnh – góc – cạnh
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Lời giải chi tiết
a) Do \(AB//CD\) nên \(\frac{{BG}}{{AG}} = \frac{{GD}}{{GC}}\).
Mặt khác \(AG = CE,BG = DF\) nên \(\frac{{DF}}{{CE}} = \frac{{GD}}{{GC}}\).
Mà \(\widehat {GDF} = \widehat {GCE}\) nên \(\Delta FDG\backsim \Delta ECG\).
b) Vì \(\Delta FDG\backsim \Delta ECG\) nên \(\widehat {DGF} = \widehat {CGE}\) và \(\frac{{DG}}{{GF}} = \frac{{GC}}{{GE}}\).
\(\widehat {DGF} = \widehat {CGE} = > \widehat {DGF} + \widehat {FGC} = + \widehat {FGC}\).
Hay \(\widehat {DGC} = \widehat {FGE}\).
Từ đó, ta có \(\Delta GDC\backsim \Delta GFE\) vì \(\frac{DG}{GF}=\frac{GC}{GE}\) và \(\widehat{DGC}=\widehat{FGE}\).
c) Vì \(\Delta GDC\backsim \Delta GFE\) nên \(\widehat {GFE} = \widehat {GDC} = 90^\circ \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 41 trang 75 sách bài tập toán 8 – Cánh diều timdapan.com"







