Bài 39 trang 87 Vở bài tập toán 7 tập 2
Giải bài 39 trang 87 vở bài tập toán 7 tập 2. Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh ...
Đề bài
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(G\) là trọng tâm, \(I\) là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó (h. 37). Chứng minh ba điểm \(A, G, I\) thẳng hàng.
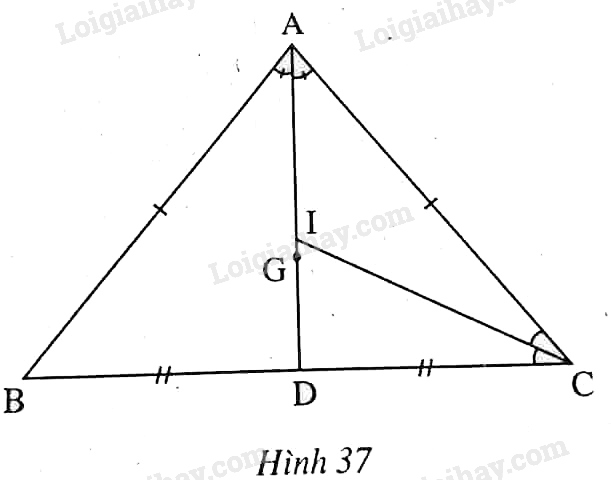
Phương pháp giải - Xem chi tiết
Áp dụng tính chất ba đường phân giác trong tam giác và trọng tâm của tam giác.
Lời giải chi tiết
Tam giác \(ABC\) cân tại \(A\) nên \(AD\) là đường phân giác đồng thời là đường trung tuyến của tam giác.
Theo giả thiết, \(G\) là trọng tâm của tam giác \(ABC\) nên \(G\) thuộc đường trung tuyến \(AD\).
Theo giả thiết, \(I\) là điểm nằm trong tam giác và cách đều ba cạnh của tam giác nên \(I\) là điểm chung của ba đường phân giác của tam giác \(ABC\), suy ra \(I\) thuộc đường phân giác \(AD\).
\(G \in AD,\) \(I \in AD,\) \( \Rightarrow A,G,I\) thẳng hàng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 39 trang 87 Vở bài tập toán 7 tập 2 timdapan.com"







