Giải bài 38 trang 92 SBT toán 10 - Cánh diều
Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính
Đề bài
Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính
a) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\)
b) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Phương pháp giải - Xem chi tiết
Bước 1: Biến đổi hiệu/ tổng 2 vectơ tương ứng thành một vectơ có giá là các cạnh của ∆ABC
Bước 2: Tính độ dài các cạnh rồi suy ra độ dài vectơ tương ứng
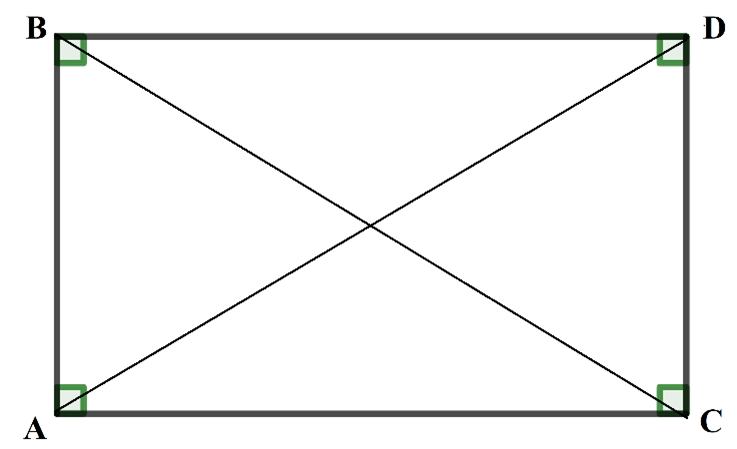
Bước 3: Dựng hình chữ nhật ABDC, sử dụng quy tắc hình bình hành để tính độ dài tổng 2 vectơ chung gốc
Lời giải chi tiết
∆ABC vuông tại A, \(AB = 4a,AC = 5a\) \( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt {41} \)
a) Ta có: \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\sqrt {41} \)
b) Dựng hình chữ nhật ABCD. Khi đó \(AD = BC = a\sqrt {41} \)
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt {41} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 38 trang 92 SBT toán 10 - Cánh diều timdapan.com"







