Bài 38 trang 162 SBT toán 8 tập 1

Đề bài

Diện tích hình bình hành bằng 24 \(c{m^2}\). Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng \(2\,cm\) và \(3\,cm.\) Tính chu vi của hình bình hành đó.

Lời giải chi tiết

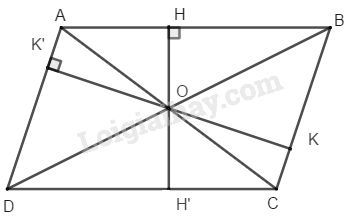
Gọi \(O\) là giao điểm hai đường chéo hình bình hành \(ABCD,\) khoảng cách từ \(O\) đến cạnh \(AB\) là \(OH = 2cm,\) đến cạnh \(BC\) là \(OK = 3cm.\)

Kéo dài \(OH\) cắt cạnh \(CD\) tại \(H’\)

\(OH ⊥ AB ⇒ OH’ ⊥ CD\) và \(OH’ = 2cm\)

nên \(HH’\) bằng đường cao của hình bình hành

\(\eqalign{  & {S_{ABCD}} = HH'.AB  \cr  &  \Rightarrow AB = {{{S_{ABCD}}} \over {HH'}} = {{24} \over 4} = 6(cm) \cr} \)

Kéo dài \(OK\) cắt \(AD\) tại \(K’\)

\(OK ⊥ BC ⇒ OK’ ⊥ AD\) và \(OK’ = 3\, (cm)\)

nên \(KK’\) là đường cao của hình bình hành

\({S_{ABCD}} = KK'.BC \\\Rightarrow BC = \eqalign{{{S_{ABCD}}} \over {KK'}} = \eqalign{{24} \over 6} = 4\) \((cm)\)

Chu vi hình bình hành \(ABCD\) là:

\((6 + 4) . 2 = 20\) \((cm)\)