Bài 35 trang 161 SBT toán 8 tập 1
Giải bài 35 trang 161 sách bài tập toán 8. Tính diện tích của một hình thang vuông, biết hai đáy có độ dài là 2cm và 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng 45 độ.
Đề bài
Tính diện tích của một hình thang vuông, biết hai đáy có độ dài là \(2\,cm\) và \(4\,cm,\) góc tạo bởi một cạnh bên và đáy lớn có số đo bằng \(45^0.\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích hình thang: \(S=\dfrac{a+b}{2}.h\) với \(a;b\) là độ dài hai đáy và \(h\) là chiều cao của hình thang.
Lời giải chi tiết
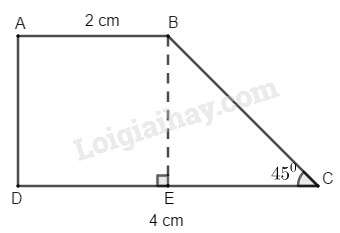
Xét hình thang vuông \(ABCD\) có:
\(\widehat A = \widehat D = {90^0};\widehat C = {45^0}\)
Kẻ \(BE ⊥ CD\)
Trong tam giác vuông \(BEC\) có \(\widehat {BEC} = {90^0}\)
\(\widehat C = 45^\circ \Rightarrow \)\(∆ BEC\) vuông cân tại \(E\)
\(⇒ BE = EC\)
Hình thang \(ABED\) có hai cạnh bên \(AD // BE\) (vì cùng vuông góc với \(DC\))
\(⇒ DE = AB = 2\,cm\)
\(EC = DC – DE = 4 – 2 = 2 \,(cm)\) \(⇒ BE = 2\,cm\)
\({S_{ABCD}} = \dfrac {1}{2}.BE\left( {AB + CD} \right)\) \(= \dfrac {1}{2}.2.\left( {2 + 4} \right) = 6(c{m^2})\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 35 trang 161 SBT toán 8 tập 1 timdapan.com"







